题目内容
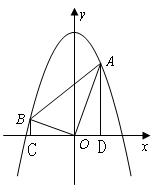
如图,已知平面直角坐标系![]() 中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结
中,点A(2,m),B(-3,n)为两动点,其中m﹥1,连结![]() ,
,![]() ,作
,作![]() 轴于
轴于![]() 点,
点,![]() 轴于
轴于![]() 点.
点.
1.求证:mn=6
2.当![]() 时,抛物线经过
时,抛物线经过![]() 两点且以
两点且以![]() 轴为对称轴,求抛物线对应的二次函数的关系式
轴为对称轴,求抛物线对应的二次函数的关系式
3.在(2)的条件下,设直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于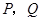 两点,问是否存在直线
两点,问是否存在直线![]() ,使S⊿POF:S⊿QOF=1:2?若存在,求出直线
,使S⊿POF:S⊿QOF=1:2?若存在,求出直线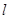 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.
1.![]() 点坐标分别为(2,m),(-3,n),∴BC=n,OC=3,OD=2,AD=m,
点坐标分别为(2,m),(-3,n),∴BC=n,OC=3,OD=2,AD=m,
又![]() ,易证
,易证![]() ,∴
,∴![]() ,∴
,∴![]() ,∴mn=6.
,∴mn=6.
2.由(1)得,![]() ,又
,又![]() ∴
∴![]()
即![]() ∴
∴![]() ,又
,又![]() ,∴
,∴![]() ,又∵mn=6, ∴
,又∵mn=6, ∴![]() ∴m=6(
∴m=6( ),n=1
),n=1
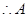 坐标为
坐标为![]() 坐标为
坐标为![]() ,易得抛物线解析式为
,易得抛物线解析式为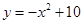 .
.
3.直线![]() 为
为![]() ,且与y轴交于
,且与y轴交于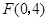 点,
点,![]()
假设存在直线![]() 交抛物线于
交抛物线于![]() 两点,且使S⊿POF:S⊿QOF=1:2,如图所示,
两点,且使S⊿POF:S⊿QOF=1:2,如图所示,
则有PF:FQ=1:2,作![]() 轴于M点,
轴于M点,![]() 轴于
轴于![]() 点,
点,
![]() 在抛物线
在抛物线![]() 上,
上,![]() 设
设![]() 坐标为
坐标为![]() ,
,
则FM=![]() ,易证△PMF∽QNF,∴
,易证△PMF∽QNF,∴![]() ,
,
∴QN=2PM=-2t,NF=2MF=![]() ,∴
,∴![]()
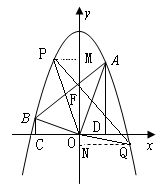
![]() 点坐标为
点坐标为![]() ,Q点在抛物线
,Q点在抛物线![]() 上,
上,
![]() ,解得
,解得![]() ,
,
![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]() ,
,
![]() 易得直线
易得直线![]() 为
为![]() .
.
根据抛物线的对称性可得直线![]() 的另解为
的另解为![]() .
.
解析:(1)根据A、B的坐标,可得OC、OD、BC、AD的长,由于OA⊥OB,可证得△BOC∽△OAD,根据相似三角形所得比例线段,即可证得所求的结论.
(2)欲求抛物线的解析式,需先求出A、B的坐标;根据(1)的相似三角形,可得3OA=mOB,用OB表示出OA,代入△OAB的面积表达式中,可得到OB2的值,在Rt△BOC中,利用勾股定理可求得另外一个OB2的表达式,联立两式可得关于m、n的等式,结合(1)的结论即可求出m、n的值,从而确定A、B的坐标和抛物线的解析式.
(3)求直线l的解析式,需先求出P、Q的坐标,已知S△POF:S△QOF=1:2,由于两三角形同底不等高,所以面积比等于高的比,即P、Q两点横坐标绝对值的比,可设出点P的坐标,然后根据两者的比例关系表示出点Q的坐标,由于点Q在抛物线的图象上,可将其代入抛物线的解析式中,即可求得点P、Q的坐标,进而可利用待定系数法求得直线l的解析式.

 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
