题目内容
7、⊙O1与⊙O2外切，且它们的半径分别是方程x2-4x+3=0的两根，则两圆的圆心距为（ ）
分析：因为⊙O1与⊙O2外切，所以两圆的圆心距为两圆的半径之和，解方程x2-4x+3=0求两根之和即可．
解答：解：设⊙O1与⊙O2的半径分别为r1、r2，即方程x2-4x+3=0的两根分别为α、β，
∵⊙O1与⊙O2外切，
∴两圆的圆心距为两圆的半径之和，
又∵⊙O1与⊙O2的半径分别是方程x2-4x+3=0的两根，
∴r1+r2=α+β=4．故选C．
∵⊙O1与⊙O2外切，
∴两圆的圆心距为两圆的半径之和，
又∵⊙O1与⊙O2的半径分别是方程x2-4x+3=0的两根，
∴r1+r2=α+β=4．故选C．
点评：考查一元二次方程根与系数的关系和圆与圆的位置关系，同时考查综合应用能力及推理能力．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
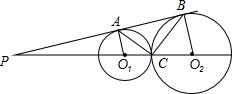公切线与两圆的切点分别为A、B，且AC=4，BC=5．
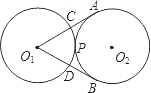如图，半径为2的两个等圆⊙O1与⊙O2外切于点P，过O1作⊙O2的两条切线，切点分别为A，B，与⊙O1分别交于C，D，则APB与CPD的弧长之和为（ ）
11、如图，已知⊙O1的半径为t，t的半径为2，圆心距O1O2=4．现把⊙O1沿直线O1O2平移，使⊙O1与⊙O2外切，则⊙O1平移的距离为（ ）
切⊙O1于点B，切⊙O2于点A，交y轴于点C（0，2），交x轴于点M．BO的延长线交⊙O2于点D，且OB：OD=1：3．