题目内容
 如图,CD是Rt△ABC斜边AB上的高,AD=4cm,BD=9cm,则CD=
如图,CD是Rt△ABC斜边AB上的高,AD=4cm,BD=9cm,则CD=
- A.6cm
- B.36cm
- C.2
 cm
cm - D.5cm
A
分析:由CD是Rt△ABC斜边AB上的高,易证得△ACD∽△CBD,由相似三角形的对应边成比例,即可求得CD的长.
解答:∵CD是Rt△ABC斜边AB上的高,
∴∠ADC=∠BDC=90°,
∴∠B+∠BCD=90°,∠BCD+∠ACD=90°,
∴∠B=∠ACD,
∴△ACD∽△CBD,
∴ ,
,
∵AD=4cm,BD=9cm,
∴ ,
,
∴CD=6cm.
故选A.
点评:此题考查了相似三角形的判定与性质.此题难度不大,解题的关键是注意方程思想与数形结合思想的应用.
分析:由CD是Rt△ABC斜边AB上的高,易证得△ACD∽△CBD,由相似三角形的对应边成比例,即可求得CD的长.
解答:∵CD是Rt△ABC斜边AB上的高,
∴∠ADC=∠BDC=90°,
∴∠B+∠BCD=90°,∠BCD+∠ACD=90°,
∴∠B=∠ACD,
∴△ACD∽△CBD,
∴
 ,
,∵AD=4cm,BD=9cm,
∴
 ,
,∴CD=6cm.
故选A.
点评:此题考查了相似三角形的判定与性质.此题难度不大,解题的关键是注意方程思想与数形结合思想的应用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
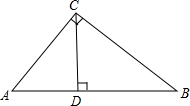 如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )
如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( ) 18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于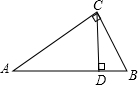 如图,CD是Rt△ABC斜边上的高线,若sinA=
如图,CD是Rt△ABC斜边上的高线,若sinA=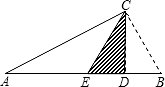 如图,CD是Rt△ABC斜边AB上的高,直角边AC=
如图,CD是Rt△ABC斜边AB上的高,直角边AC=