题目内容
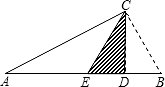 如图,CD是Rt△ABC斜边AB上的高,直角边AC=2
如图,CD是Rt△ABC斜边AB上的高,直角边AC=2| 3 |
分析:先根据图形折叠的性质得出阴影部分的面积等于△CED的面积,再由直角三角形斜边的中线等于斜边的一半即可得出CE=AE,进而可判断出△BEC是等边三角形,由等边三角形的性质及直角三角形的性质,三角形的面积公式即可得出结论.
解答:解:△ABC沿CD折叠B与E重合,
则BC=CE,
∵E为AB中点,△ABC是直角三角形,
∴CE=BE=AE,
∴△BEC是等边三角形.
∴∠B=60°,
∴∠A=30°,
∵AC=2
,
∴CD=
,
∴ED=1.
∴阴影部分的面积=
×
×1=
.
故答案为:
.
则BC=CE,
∵E为AB中点,△ABC是直角三角形,
∴CE=BE=AE,
∴△BEC是等边三角形.
∴∠B=60°,
∴∠A=30°,
∵AC=2
| 3 |
∴CD=
| 3 |
∴ED=1.
∴阴影部分的面积=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:考查直角三角形的性质,等边三角形的判定及图形折叠等知识的综合应用能力及推理能力.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
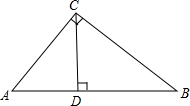 如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )
如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( ) 18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于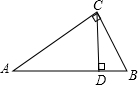 如图,CD是Rt△ABC斜边上的高线,若sinA=
如图,CD是Rt△ABC斜边上的高线,若sinA=