Question

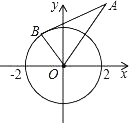
【题目】如图，⊙O的半径为2，点A的坐标为（2，2），直线AB为⊙O的切线，B为切点．则B点的坐标为_______．

Answer 1

【答案】

【解析】

过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，先利用切线AC求出OC＝2＝OA，从而∠BOD＝∠AOC＝60°，利用30°所对直角边是斜边一半,即可求出B点的坐标．

解：过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，

∵⊙O的半径为2，点A的坐标为（2，2），即OC＝2，

∴AC是圆的切线．

∵点A的坐标为（2，2），

∴OA＝＝4，

∵BO＝2，AO＝4，∠ABO＝90°，

∴∠AOB＝60°，

∵OA＝4，OC＝2，

∴sin∠OAC＝，

∴∠OAC＝30°，

∴∠AOC＝60°，即∠AOB＝∠AOC＝60°，

∴∠BOD＝180°﹣∠AOB﹣∠AOC＝60°，

∴OD＝1，BD＝，即B点的坐标为（﹣1，）．