题目内容
已知二元一次方程组 的解是
的解是 ,求关于x,y的二元一次方程ax-by=2的自然数解.
,求关于x,y的二元一次方程ax-by=2的自然数解.
解:依题意得: ,
,
将①×3+②得,44a=22,即a= ,
,
代入①得,b= .
.
将a、b代入方程ax-by=2,得
 =2,
=2,
即x+y=4.
∴方程的解为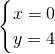 ,
, ,
, ,
, ,
, .
.
分析:先把x=4,y=5代入方程组中得到a,b的二元一次方程组,解出a,b的值,再把a、b的值代入ax-by=2中,把x或y从0开始递增对应地解出y或x的值.
点评:本题考的是二元一次方程的解,先运用代入法和加减消元法求出a、b的值,再代入方程ax-by=2中求x,y的值.
要注意的是,学生在解此题时常常会忽略0的情况.
 ,
,将①×3+②得,44a=22,即a=
 ,
,代入①得,b=
 .
.将a、b代入方程ax-by=2,得
 =2,
=2,即x+y=4.
∴方程的解为
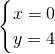 ,
, ,
, ,
, ,
, .
.分析:先把x=4,y=5代入方程组中得到a,b的二元一次方程组,解出a,b的值,再把a、b的值代入ax-by=2中,把x或y从0开始递增对应地解出y或x的值.
点评:本题考的是二元一次方程的解,先运用代入法和加减消元法求出a、b的值,再代入方程ax-by=2中求x,y的值.
要注意的是,学生在解此题时常常会忽略0的情况.

练习册系列答案
相关题目
 的解的和是2,求x、y、k的值。
的解的和是2,求x、y、k的值。 的解为正数。
的解为正数。 。
。 的解为正数。
的解为正数。 。
。 的解的和是2,求x、y、k的值。
的解的和是2,求x、y、k的值。 的解是
的解是 ,则
,则 的值是
的值是