题目内容
设同一个圆的内接正六边形、正八边形、正十二边形的边心距分别为r6,r8,r12,则r6,r8,r12的大小关系为( )
A.r6>r8>r12 B.r6<r8<r12 C.r8>r6>r12 D.不能确定
B【考点】正多边形和圆.
【分析】圆的内接正多边形,边数越多,多边形就和圆越接近,则边心距就越接近圆的半径.
【解答】解:根据同一个圆的内接正多边形的特点得:r6<r8<r12;
故选:B.
【点评】本题考查了正多边形和圆;熟记正多边形的边数越多,就越接近外接圆,边心距越大是解决问题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目


 a2﹣2ab)﹣2(6a2﹣5ab),其中a=﹣
a2﹣2ab)﹣2(6a2﹣5ab),其中a=﹣ ,b=2.
,b=2.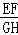 的值是( )
的值是( )
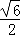 B.
B.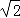 C.
C.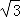 D.2
D.2