题目内容
在⊙O中,直径AB=4,弦CD⊥AB,垂足为E,若OE= ,则CD的长为________.
,则CD的长为________.
2
分析:根据题意画出图形,连接OC,由AB=4求出OC的长,在Rt△OCE中利用勾股定理求出CE的长,再根据CD=2CE即可得出结论.
解答: 解:如图所示:
解:如图所示:
∵直径AB=4,弦CD⊥AB,垂足为E,OE= ,
,
∴OC= AB=
AB= ×4=2,
×4=2,
∴CE=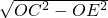 =
= =1,
=1,
∵AB⊥CD,
∴CD=2CE=2×1=2.
故答案为:2.
点评:本题考查的是垂径定理及勾股定理,根据题意画出图形,构造出直角三角形是解答此题的关键.
分析:根据题意画出图形,连接OC,由AB=4求出OC的长,在Rt△OCE中利用勾股定理求出CE的长,再根据CD=2CE即可得出结论.
解答:
 解:如图所示:
解:如图所示:∵直径AB=4,弦CD⊥AB,垂足为E,OE=
 ,
,∴OC=
 AB=
AB= ×4=2,
×4=2,∴CE=
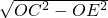 =
= =1,
=1,∵AB⊥CD,
∴CD=2CE=2×1=2.
故答案为:2.
点评:本题考查的是垂径定理及勾股定理,根据题意画出图形,构造出直角三角形是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.
22、如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°. 直线AB相交于点G.
直线AB相交于点G.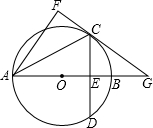 C与直线AB相交于点G.
C与直线AB相交于点G. 如图,在⊙O中,直径AB⊥弦CD于E,连接BD,若∠D=30°,BD=2,则AE的长为( )
如图,在⊙O中,直径AB⊥弦CD于E,连接BD,若∠D=30°,BD=2,则AE的长为( )