题目内容
如图,抛物线 经过点A、B、C,已知A(-1,0),C(0,3).P为线段BC上一点,过点P作
经过点A、B、C,已知A(-1,0),C(0,3).P为线段BC上一点,过点P作 轴平行线,交抛物线于点D,当△BDC的面积最大时,点P的坐标为 .
轴平行线,交抛物线于点D,当△BDC的面积最大时,点P的坐标为 .

( ,
, ).
).
【解析】
试题分析:把点A、C的坐标代入抛物线解析式求出b、c的值,从而得到抛物线的解析式,再求出点B的坐标,然后利用待定系数法求出直线BC的解析式,当与BC平行的直线与抛物线有且只有一个交点时,点D到BC的距离最大,此时△BDC的面积最大,然后联立直线与抛物线解析式,消掉y得到关于x的一元二次方程,利用根与系数的关系求出x的值,即可得到点D的横坐标,然后代入直线BC的解析式求出点P的纵坐标,即可得解;
试题解析:∵抛物线y=-x2+bx+c经过点A(-1,0),C(0,3),
∴
解得 ,
,
∴y=-x2+2x+3,
令y=0,则-x2+2x+3=0,
解得x1=-1,x2=3,
∴点B的坐标为(3,0),
设直线BC的解析式为y=kx+b,
则 ,
,
解得 ,
,
所以,直线BC的解析式为y=-x+3,
过点D作BC的平行直线,设解析式为y=-x+d,
联立 ,
,
消掉y得,-x2+2x+3=-x+d,
整理得,x2-3x-3+d=0,
当△=0时,方程有两个相等的实数根,此时点D到BC的距离最大,△BDC的面积最大,
所以,x=- ,
,
∵PD∥y轴,
∴点P的横坐标为 ,
,
此时y=- +3=
+3= ,
,
∴点P的坐标为( ,
, ).
).
考点:二次函数综合题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 时,下列函数:①
时,下列函数:① ;②
;② ;③
;③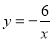 ;④
;④ ,函数值
,函数值 随自变量
随自变量 增大而增大的有( )
增大而增大的有( )
 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论:
 ;
; ;
; ;
; ;
; ,(
,( 的实数)
的实数) 与二次函数
与二次函数 的图象上.
的图象上.
 和
和 ,
, 的值;
的值; >
> 时,自变量
时,自变量 的取值范围.
的取值范围. C.13或
C.13或 D.13或12
D.13或12 ,其顶点坐标是( )
,其顶点坐标是( ) B.
B. C.
C. D.
D.