Question

【题目】如图，矩形中，点是线段上一动点，为的中点，的延长线交于．

求证：；

若厘米，厘米，当为何值时，四边形是菱形，并加以说明．

Answer 1

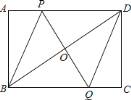
【答案】（1）证明见解析；（2）当为厘米时，四边形是菱形．

【解析】

（1）根据矩形性质推出AD∥BC，根据平行线的性质得出∠PDO=∠QBO，根据全等三角形的判定ASA证△PDO≌△BQO，根据全等三角形的性质推出即可．
（2）由菱形的性质得出BP=PD，设AP=x厘米，则BP=PD=（4-x）厘米，由勾股定理得出方程，解方程即可．

证明：∵四边形是矩形，

∴，，

∴，

∵为中点，

∴，

在和中，

，

∴，

∴．

解：当时，四边形是菱形；理由如下：

∵，，

∴四边形是平行四边形，

当四边形是菱形时，，

设厘米，则厘米，

由勾股定理得：，

解得：，

即当为厘米时，四边形是菱形．