题目内容

直角梯形OABC中，BC∥OA，∠OAB=90°，OA=4，腰AB上有一点D，AD=2，四边形ODBC的面积为6，建立如图所示的直坐标系，反比例函数y= $数学公式$ （x＞0）的图象恰好经过点C和点D，则CB与BD的比值是

A.
1
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

D
分析：先设点C（x， $\text{[math]}$ ），后由梯形面积得到x的值，又由BC等于4-x，BD等于 $\text{[math]}$ ，从而解得．
解答：

解：由题意点D（4，2），
代入双曲线方程得：m=8，
由题意设点C（x， $\text{[math]}$ ），则AB= $\text{[math]}$ ，BC=4-x，
梯形ABCO的面积= $\text{[math]}$ =2×4× $\text{[math]}$ +6，
即 $\text{[math]}$ = $\text{[math]}$ =20，
解得：x= $\text{[math]}$ ，
所以点C（ $\text{[math]}$ ），
所以BC=4-x= $\text{[math]}$ ，BD= $\text{[math]}$ = $\text{[math]}$ ，
所以 $\text{[math]}$ ．
故选D．
点评：本题考查了反比例函数的综合应用，通过设点C，用点C坐标表示BC，BD的长度，通过求梯形面积可以求得x的值，从而解得．

练习册系列答案

学优冲刺100系列答案

名校秘题小学毕业升学系统总复习系列答案

名师面对面小考满分策略系列答案

教材全解字词句篇系列答案

课时练全优达标测试卷系列答案

万唯中考试题研究系列答案

1课3练世界图书出版公司系列答案

学生用书系列答案

全优训练系列答案

语文阅读阶梯训练系列答案

相关题目

如图，直角梯形OABC中，AB∥OC，O为坐标原点，点A在y轴正半轴上，点C在x轴正半轴上，点B坐标为（2，2

），∠BCO=60°，OH⊥BC于点H．动点P从点H出发，沿线段HO向点O运动，

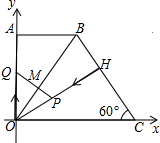动点Q从点O出发，沿线段OA向点A运动，两点同时出发，速度都为每秒1个单位长度．设点P运动的时间为t秒．
（1）求OH的长；
（2）若△OPQ的面积为S（平方单位）．求S与t之间的函数关系式．并求t为何值时，△OPQ的面积最大，最大值是多少；
（3）设PQ与OB交于点M．
①当△OPM为等腰三角形时，求（2）中S的值．
②探究线段OM长度的最大值是多少，直接写出结论．

如图，在直角梯形OABC中，CB∥OA，∠OAB=90°，点O为坐标原点，点A在x轴的

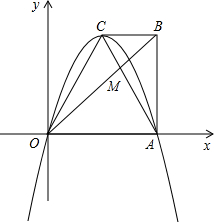正半轴上，对角线OB，AC相交于点M，OA=AB=4，OA=2CB．
（1）点C的坐标为

；
（2）求△OCM的面积；
（3）若点E在过O，A，C三点的抛物线的对称轴上，点F为该抛物线上的点，且以A，O，F，E四点为顶点的四边形为平行四边形，求点F的坐标．

做一做
（1）在直角坐标系中描出下列各组点，并将各组内的点用线段依次连接起来．

（1）（1，0）、（6，0）、（6，1）、（5，0）、（6，-1）、（6，0）；
（2）（2，0）、（5，3）、（4，0）；
（3）（2，0）、（5，-3）、（4，0）．
观察所得到的图形像什么？如果要将此图形向上平移到x轴上方，那么至少要向上平移几个单位长度．

（2）如图，AD是∠EAC的平分线，AD∥BC，∠B=45°，则∠DAC的度数是多少？
（写出解答过程）

（3）如图所示的平面直角坐标系，在直角梯形OABC中，CB∥OA，CB=8，OC=8，∠OAB=45°

（1）求点A、B、C的坐标；
（2）求梯形OABC的面积．

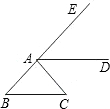
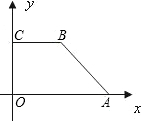
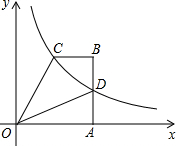直角梯形OABC中，BC∥OA，∠OAB=90°，OA=4，腰AB上有一点D，AD=2，四边形ODBC的面积为6，建立如图所示的直坐标系，反比例函数y=

（x＞0）的图象恰好经过点C和点D，则CB与BD的比值是（　　）

如图，直角梯形OABC中，AB∥OC，O为坐标原点，点A在y轴正半轴上，点C在x轴正半轴上，点B坐标为（2，2

），∠BCO=60°，OH⊥BC于点H，动点P从点H出发，沿线段HO向点O运动，动点Q从点O出发，沿线段OA向点A运动，两点同时出发，速度都为每秒1个单位长度，设点P运动的时间为t秒．
（1）OH=

；
（2）用含t（秒）的代数式表示点P和Q的坐标：P（

）；
（3）若△OPQ的面积为S（平方单位），求S与t之间的函数关系，并求t为何值时，△OPQ的面积最大，最大值是多少？