题目内容
16.某商场将每件进价为20元的玩具以单价为30元的价格出售时,每天可售出300件,经调查当单价每涨1元时,每天少售出10件.若商场想每天获得3750元利润,则每件玩具应涨多少元?这道应用题如果设每件玩具应涨x元,则下列说法错误的是( )| A. | 涨价后每件玩具的售价是(30+x)元 | |
| B. | 涨价后每天少售出玩具的数量是10x件 | |
| C. | 涨价后每天销售玩具的数量是(300-10x)件 | |
| D. | 可列方程为(30+x)(300-10x)=3750 |
分析 设涨价x元,然后分别表示出销量和涨价后的单价即可列出方程求解.
解答 解:设涨价x元,根据题意可得:
A、∵(30+x)表示涨价后玩具的单价,∴A选项正确;
B、∵10x表示涨价后少售出玩具的数量,∴B选项正确;
C、∵(300-10x)表示涨价后销售玩具的数量,∴C选项正确;
D、∵可列方程(30+x-20)(300-10x)=3750,故D选项错误,
故选D.
点评 本题考查了由实际问题抽象出一元二次方程的知识,解题的关键是能够分别表示出单件利润和总的销售量,从而表示出总利润.

练习册系列答案
相关题目
7.方程x2-3x=0根是( )
| A. | x=-3 | B. | x1=0,x2=-3 | C. | x=3 | D. | x1=0,x2=3 |
5.一个暗箱里装有5个黑球,3个白球,1个红球,每个球除颜色外都相同,从中任意摸出一个球,摸到白球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{8}$ | C. | $\frac{4}{15}$ | D. | $\frac{4}{11}$ |
6.下列命题是假命题的有( )
①邻补角相等;②对顶角相等;③同位角相等;④内错角相等.
①邻补角相等;②对顶角相等;③同位角相等;④内错角相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,点A的坐标为(-3,0),点B在直线y=-x上运动,连接AB,当线段AB最短时,点B坐标为(-1.5,1.5).
如图,点A的坐标为(-3,0),点B在直线y=-x上运动,连接AB,当线段AB最短时,点B坐标为(-1.5,1.5).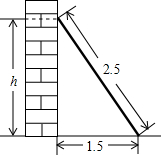 如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,则梯子的顶端与地面的距离为2m.
如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,则梯子的顶端与地面的距离为2m.