题目内容
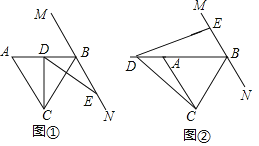
【题目】如图，在平行四边形
中，过
点作
于点
，过
上一点
作
于点
，交
于点
，连接
过作
于点
，连接
．
（1）若
，
，求的长；
（2）若
，求证：
．
【答案】(1)9
(2)证明见解析
【解析】
(1)∵
，
∴
(2) 先做辅助线，作EM
AC于M，
交GF的延长线于N，连接AF
已知
，求证：
，将AG=AM+MG，GF=GN-FN代入可得
AM+MG+GN-FN=
，若使等式成立，只要证得AM，，MG，GN，FN，EG之间的关系即可，
其中就要利用三角形全等推出对应边相等，即可求证.
(1)∵，
∴
(2)证明：如图，作EM AC于M，交GF的延长线于N，连接AF
在
和
中
∴
∴
(AAS)
∴AE=EF=9
∵
∴
且
又∵
∴E，F，G，C四点共圆，
∴
∴EM=EN，MG=GN
∴
∴AM=FN
AG+FG=AM+MG+GN-NF=2MG
在
中
∴
∴AG+FG=
练习册系列答案
相关题目
