题目内容
已知关于一元二次方程(x－m)2＋6x＝4m－3有实数根．
(1)
求m的取值范围；
(2)设方程的两实数根分别为x1与x2，求
x1·x2－x
－x
的最大值．
解：(1)由(x－m)2＋6x＝4m－3，得
x2＋(6－2m)x＋m2－4m＋3＝0.
∴Δ＝b2－4ac＝(6－2m)2－4×1×(m2－4m＋3)＝－8m＋24.(2分)
∵方程有实数根，∴－8m＋24≥0，解得m≤3，∴m的取值范围是m≤3
(2)∵方程的两实根分别为x1与x2，
∴x1＋x2＝2m－6，x1·x2＝m2－4m＋3，
∴x1·x2－x－x＝3x1·x2－(x1＋x2)2
＝3(m2－4m＋3)－(2m－6)2＝－m2＋12m－27＝－(m－6)2＋9.
∵m≤3，且当m＜6时，－(m－6)2＋9的值随m的增大而增大，
∴当m＝3时，x1·x2－x－x的值最大，最大值为－(3－6)2＋9＝0，
∴x1·x2－x－x的最大值为0.
练习册系列答案
快乐5加2金卷系列答案
相关题目
时针方向旋转到△BCF，则旋转角是( )
，若
随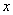
的增大而增大，则
的值可以是（ ）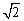
R C．
R D．
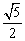R
