题目内容
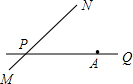如图，公路PQ和公路MN交于点P，且∠NPQ=30°，公路PQ上有一所学校A，AP=160米，若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响，假设拖拉机行驶时周围100米以内会受到噪声的影响，则造成影响的时间为分析：设AC、AD为正好受影响时，则AC=AD=100，在Rt△ABC中，BC2=AC2-AB2=3600，由此可以求出BC，BD，又拖拉机速度为18米∕秒，让路程除以速度可以计算出受影响时间．
解答：
解：作AB⊥DP于B，
则AB为A到道路的最短距离．
在Rt△APB中，
∵∠NPQ=30°，
∴sin30°=
，
∴AB=APsin30°=80（米），
在Rt△ABD中，BD=
=60（米），
∴受影响的时间为：（60×2）÷18=
秒，
故答案为
．
解：作AB⊥DP于B，则AB为A到道路的最短距离．
在Rt△APB中，
∵∠NPQ=30°，
∴sin30°=
| AB |
| AP |
∴AB=APsin30°=80（米），
在Rt△ABD中，BD=
| 1002-802 |
∴受影响的时间为：（60×2）÷18=
| 20 |
| 3 |
故答案为
| 20 |
| 3 |
点评：解此题的关键是把实际问题转化为数学问题，把实际问题抽象到解直角三角形中，进行解答；注意运用等腰三角形三线合一的性质得到受影响的路程．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
如图，公路MN和公路PQ在点P处交汇，且∠QPN=30°．点A处有一所中学，AP=160m，一辆拖拉机从P沿公路MN前行，假设拖拉机行驶时周围100m以内会受到噪声影响，那么该所中学是否会受到噪声影响，请说明理由，若受影响已知拖拉机的速度为18km/h，那么学校受影响的时间为多长？
如图，公路PQ和公路MN交于点P，且∠NPQ=30°，公路PQ上有一所学校A，AP=160米，若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响，假设拖拉机行驶时周围100米以内会受到噪声的影响，则造成影响的时间为________秒．
公路PQ上有一所学校A,AP=160米，若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响， 则造成影响的时间为 秒。 