题目内容
某水渠的横截面呈抛物线形,水面的宽为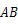 (单位:米),现以
(单位:米),现以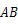 所在直线为
所在直线为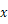 轴,以抛物线的对称轴为
轴,以抛物线的对称轴为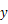 轴建立如图所示的平面直角坐标系,设坐标原点为
轴建立如图所示的平面直角坐标系,设坐标原点为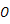 .已知
.已知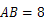 米,设抛物线解析式为
米,设抛物线解析式为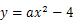 .
.
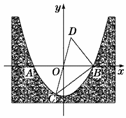
第21题图
(1)求 的值;
的值;
(2)点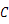 (-1,
(-1,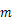 )是抛物线上一点,点
)是抛物线上一点,点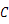 关于原点
关于原点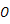 的对称点为
的对称点为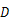 ,连接
,连接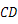 ,
,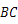 ,
,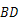 ,求△
,求△ 的面积.
的面积.
分析:(1)求出点A或点B的坐标,将其代入,即可求出a的值;
(2)把点代入(1)中所求的抛物线的解析式中,求出点C的坐标,再根据点C和点D关于原点O对称,求出点D的坐标,然后利用求△BCD的面积.
解:(1)∵ ,由抛物线的对称性可知,
∴ (4,0).∴ 0=16a-4.∴ a.
(2)如图所示,过点C作于点E,过点D作于点F.
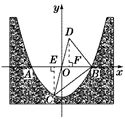
第21题图
∵ a=,∴ -4.当-1时,m=×-4=-,∴ C(-1,-).
∵ 点C关于原点O的对称点为D,
∴ D(1,).∴ .
∴ ×4×+×4×=15.
∴ △BCD的面积为15平方米.
点拨:在直角坐标系中求图形的面积,常利用“割补法”将其转化为有一边在坐标轴上的图形面积的和或差求解.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 B.2+
B.2+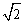 =2
=2 =2
=2 =
=

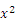 +x+c的图象与x轴有两个交点A(
+x+c的图象与x轴有两个交点A(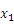 ,0),A(
,0),A(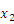 ,0),且
,0),且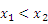 ,点P(m,n)是图象上一点,那么下列判断正确的是( )
,点P(m,n)是图象上一点,那么下列判断正确的是( )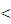 0时,m
0时,m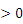 时,m>
时,m>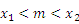 D.当n
D.当n 的图象是由函数
的图象是由函数 的图象先向 (左、右)平移
的图象先向 (左、右)平移 B.
B. C.a3·a3=a6 D.(-2a2)3=-6a6
C.a3·a3=a6 D.(-2a2)3=-6a6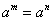 (
( 且
且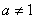 ,m、n是正整数),则m = n”.你能利用上面的结论解决下面的问题吗?试试看,相信你一定行!
,m、n是正整数),则m = n”.你能利用上面的结论解决下面的问题吗?试试看,相信你一定行!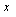 =39,求x 的值; (2)如果2÷8
=39,求x 的值; (2)如果2÷8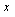 ·16
·16