题目内容
 如图,一块含30°角的直角三角板,它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是________cm.
如图,一块含30°角的直角三角板,它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是________cm.
6
分析:连接BE,作EN⊥BC,FM⊥BC,即可求得EF的长,则在直角△DEF中,即可解得DE,DF的长,从而求得三角形的周长.
解答: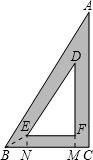 解:连接BE,作EN⊥BC,FM⊥BC,则CM=1cm.
解:连接BE,作EN⊥BC,FM⊥BC,则CM=1cm.
∵直角△ABC中,∠A=30°,
∴BC= AB=
AB= ×8=4.
×8=4.
∵E到AB与到BC的距离相等,
∴BE平分∠ABC.
∴∠EBN=30°
在直角△BNE中,tan∠EBN= .
.
∴BN=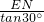 =
= EN=
EN= .
.
∴EF=NM=4-BN-CM=4- -1=3-
-1=3- .
.
在直角△DEF中,∠D=30°,
∴DE=2EF=6-2 ,
,
DF= EF=3
EF=3 -3.
-3.
∴△DEF的周长是EF+DE+DF=3- +6-2
+6-2 +3
+3 -3=6.
-3=6.
故答案是:6.
点评:本题考查了含30°锐角的直角三角形的性质,关键是作出辅助线求得EF的长.
分析:连接BE,作EN⊥BC,FM⊥BC,即可求得EF的长,则在直角△DEF中,即可解得DE,DF的长,从而求得三角形的周长.
解答:
 解:连接BE,作EN⊥BC,FM⊥BC,则CM=1cm.
解:连接BE,作EN⊥BC,FM⊥BC,则CM=1cm.∵直角△ABC中,∠A=30°,
∴BC=
 AB=
AB= ×8=4.
×8=4.∵E到AB与到BC的距离相等,
∴BE平分∠ABC.
∴∠EBN=30°
在直角△BNE中,tan∠EBN=
 .
.∴BN=
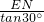 =
= EN=
EN= .
.∴EF=NM=4-BN-CM=4-
 -1=3-
-1=3- .
.在直角△DEF中,∠D=30°,
∴DE=2EF=6-2
 ,
,DF=
 EF=3
EF=3 -3.
-3.∴△DEF的周长是EF+DE+DF=3-
 +6-2
+6-2 +3
+3 -3=6.
-3=6.故答案是:6.
点评:本题考查了含30°锐角的直角三角形的性质,关键是作出辅助线求得EF的长.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图,一块含30°角的直角三角板,它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是
如图,一块含30°角的直角三角板,它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是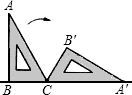 如图,一块含30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=6cm,则顶点A从开始到结束所经过的路径长为
如图,一块含30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=6cm,则顶点A从开始到结束所经过的路径长为 如图,一块含30°角的直角三角尺ABC,∠B=90°,∠A=30°,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC=5cm,那么线段BB′长为
如图,一块含30°角的直角三角尺ABC,∠B=90°,∠A=30°,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC=5cm,那么线段BB′长为 D.
D.

 如图,一块含30°角的直角三角尺ABC,∠B=90°,∠A=30°,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC=5cm,那么线段BB′长为________.
如图,一块含30°角的直角三角尺ABC,∠B=90°,∠A=30°,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC=5cm,那么线段BB′长为________.