题目内容
 如图,一块含30°角的直角三角尺ABC,∠B=90°,∠A=30°,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC=5cm,那么线段BB′长为________.
如图,一块含30°角的直角三角尺ABC,∠B=90°,∠A=30°,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC=5cm,那么线段BB′长为________.
5 cm
cm
分析:连接BB′交AC于D,由已知及旋转的性质可得∠A′CB′=∠ACB=60°,B′C=BC=5cm,所以得△BCD≌△B′CD,从而得BD=B′D且直角三角形BCD和直角三角形B′CD,由三角函数可求出BD,继而求得BB′的长.
解答:连接BB′交AC于D,
已知,∠B=90°,∠A=30°,
∴由已知及旋转的性质得:
∠A′CB′=∠ACB=60°,B′C=BC=5cm,
则∠B′CD=60°
∴△BCD≌△B′CD,
∴BD=B′D,
∴∠BDC=∠B′DC=90°,
在Rt△BDC中,
BD=BC•cos30°=5× =
= (cm),
(cm),
∴B′D= cm,
cm,
∴BB′=BD+B′D= +
+ =5
=5 (cm),
(cm),
故答案为:5 cm.
cm.
点评:本题综合考查了解直角三角形以及旋转的性质,由旋转的性质先证得△BCD≌△B′CD得出直角三角形BCD和直角三角形B′CD是关键.
 cm
cm分析:连接BB′交AC于D,由已知及旋转的性质可得∠A′CB′=∠ACB=60°,B′C=BC=5cm,所以得△BCD≌△B′CD,从而得BD=B′D且直角三角形BCD和直角三角形B′CD,由三角函数可求出BD,继而求得BB′的长.
解答:连接BB′交AC于D,
已知,∠B=90°,∠A=30°,
∴由已知及旋转的性质得:
∠A′CB′=∠ACB=60°,B′C=BC=5cm,
则∠B′CD=60°
∴△BCD≌△B′CD,
∴BD=B′D,
∴∠BDC=∠B′DC=90°,
在Rt△BDC中,
BD=BC•cos30°=5×
 =
= (cm),
(cm),∴B′D=
 cm,
cm,∴BB′=BD+B′D=
 +
+ =5
=5 (cm),
(cm),故答案为:5
 cm.
cm.点评:本题综合考查了解直角三角形以及旋转的性质,由旋转的性质先证得△BCD≌△B′CD得出直角三角形BCD和直角三角形B′CD是关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 如图,一块含30°角的直角三角板,它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是
如图,一块含30°角的直角三角板,它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是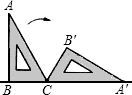 如图,一块含30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=6cm,则顶点A从开始到结束所经过的路径长为
如图,一块含30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=6cm,则顶点A从开始到结束所经过的路径长为 如图,一块含30°角的直角三角尺ABC,∠B=90°,∠A=30°,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC=5cm,那么线段BB′长为
如图,一块含30°角的直角三角尺ABC,∠B=90°,∠A=30°,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC=5cm,那么线段BB′长为 D.
D.
