题目内容
(1)求函数y1的表达式和点B的坐标；
(2)观察图象，比较当x＞0时y1与y2的大小．
(1)由题意，得
解得
∴
又A点在函数
上，所以
，解得
所以
解方程组
得
所以点B的坐标为（1, 2）
（2）当0＜x＜1或x＞2时，y1＜y2;
当1＜x＜2时，y1＞y2;
当x=1或x=2时，y1=y2.
解析
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知一次函数y1=2x，二次函数y2=x2+1．
（Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
（Ⅱ）观察第（Ⅰ）问表中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数所对应的函数值y1≤y2均成立；
（Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．
（Ⅰ）根据表中给出的x的值，计算对应的函数值y1、y2，并填在表格中：
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y1=2x | |||||||
| y2=x2+1 |
（Ⅲ）试问，是否存在二次函数y3=ax2+bx+c，其图象经过点（-5，2），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y1≤y3≤y2均成立？若存在，求出函数y3的解析式；若不存在，请说明理由．
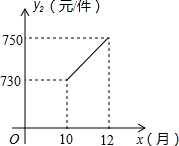某企业为杭州计算机产业基地提供电脑配件．受美元走低的影响，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y1（元）与月份x（1≤x≤9，且x取整数）之间的函数关系如下表：
某精品水果超市销售一种进口水果A，从去年1至7月，这种水果的进价一路攀升，每千克A的进价y1与月份x（1≤x≤7，且x为整数），之间的函数关系式如下表：