Question

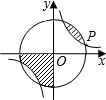如图，反比例函数y=

k

x

与⊙O的一个交点为（2，1），则图中阴影部分的面积是

5π

4

．

Answer 1

分析：根据反比例函数的图象关于坐标原点对称，是中心对称图形可得：图中两个阴影面积的和是

1

4

圆的面积，又知两图象的交点P的坐标为（2，1），即可求出圆的半径．

解答：解：∵圆和反比例函数一个交点P的坐标为（2，1），
∴可知圆的半径r=

22+12

=

5

，
∵反比例函数的图象关于坐标原点对称，是中心对称图形，
∴图中两个阴影面积的和是

1

4

圆的面积，
∴S_阴影=

( 5 )2π

4

=

5π

4

．
故答案为：

5π

4

．

点评：本题主要考查反比例函数图象的对称性的知识点，解决本题的关键是利用反比例函数的对称性得到阴影部分与圆之间的关系．