题目内容
如图，∠AOB=45°，C为∠AOB内一点，点C关于OA、OB的对称点D、E，试判断△ODE的形状是等腰直角三角形
等腰直角三角形
．分析：根据题意作出图形，连接由轴对称的性质可知，OD=OC，OE=OC，∠AOD=∠AOC，∠BOE=∠BOC，由此即可得出结论．
解答：
解：如图所示：
∵点C关于OA、OB的对称点D、E，
∴OA是线段CD的垂直平分线，OB是线段CE的垂直平分线，
∴OD=OC，OE=OC，∠AOD=∠AOC，∠BOE=∠BOC，
∴∠AOD+∠BOE=∠AOC+∠BOC=45°，即∠DOE=90°，
∴△ODE是等腰直角三角形．
故答案为：等腰直角三角形．
解：如图所示：∵点C关于OA、OB的对称点D、E，
∴OA是线段CD的垂直平分线，OB是线段CE的垂直平分线，
∴OD=OC，OE=OC，∠AOD=∠AOC，∠BOE=∠BOC，
∴∠AOD+∠BOE=∠AOC+∠BOC=45°，即∠DOE=90°，
∴△ODE是等腰直角三角形．
故答案为：等腰直角三角形．
点评：本题考查的是轴对称的性质，熟知如果两个图形的对应点的连线被同一条直线垂直平分，那么这两个图形关于这条直线对称是解答此题的关键．
练习册系列答案
相关题目
如图，∠AOB=45°，过OA上到点O的距离分别为1，3，5，7，9，11，的点作OA的垂线与OB相交，得到并标出一组黑色梯形，它们的面积分别为S1，S2，S3，S4，…，观察图中的规律，求出第10个黑色梯形的面积S10=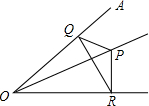
如图，∠AOB=45°，角内有点P，PO=10，在角的两边上有两点Q，R（均不同于O点），则△PQR的周长的最小值为
如图，∠AOB=45°，过OA上到点O的距离分别为1，2，3，4，5 …的点作OA的垂线与OB相交，再按一定规律标出一组如图所示的黑色梯形．设前n个黑色梯形的面积和为Sn．| n | 1 | 2 | 3 | … |
| Sn | … |
（2）已知Sn与n之间满足一个二次函数关系，试求出这个二次函数的解析式．
如图，∠AOB=45°，OC平分∠AOB，点M在OB上，且OM=
如图，∠AOB=45°，在OA上截取OA1=1，OA2=3，OA3=5，OA4=7，OA5=9，…，过点A1、A2、A3、A4、A5分别作OA的垂线与OB相交，得到并标出一组阴影部分，它们的面积分别为S1，S2，S3，…．观察图中的规律，第n个阴影部分的面积Sn为（ ）