题目内容
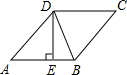如图，已知菱形ABCD的周长为20cm，DE⊥AB垂足为E，cosA=
则BD=
- A.4
- B.3
- C.
- D.2
D
分析：先由菱形的性质求出AD、AB的长度，再由cosA=可得出AE、EB的长度，进而在RT△DEB中利用勾股定理可得出BD的长度．
解答：∵菱形ABCD的周长为20cm，
∴AD=AB=BC=CD=5cm，
又∵cosA==
，
∴AE=3，DE=4，EB=AB-AE=2，
在RT△DBE中，BD=
=
=2．
故选D．
点评：此题考查了菱形的性质及勾股定理的知识，解答本题的关键是根据题意求出DE、EB的长度，另外要熟练掌握勾股定理在解直角三角形中的应用，难度一般．
分析：先由菱形的性质求出AD、AB的长度，再由cosA=
可得出AE、EB的长度，进而在RT△DEB中利用勾股定理可得出BD的长度．解答：∵菱形ABCD的周长为20cm，
∴AD=AB=BC=CD=5cm，
又∵cosA=
=，∴AE=3，DE=4，EB=AB-AE=2，
在RT△DBE中，BD=
==2．故选D．
点评：此题考查了菱形的性质及勾股定理的知识，解答本题的关键是根据题意求出DE、EB的长度，另外要熟练掌握勾股定理在解直角三角形中的应用，难度一般．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
如图，已知菱形ABCD的边长为1.5cm，B，C两点在扇形AEF的
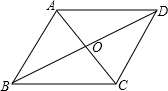如图，已知菱形ABCD的周长为16cm，∠ABC=60°，对角线AC和BD相交于点O，求AC和BD的长．
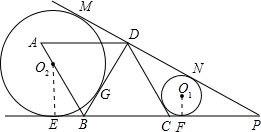上，半径为r1的圆O1与DC、CP、DP分别相切于点H、F、N，半径为r2的圆O2与PD延长线、CB延长线和BD分别相切于点M、E、G．
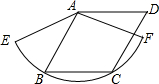如图，已知菱形ABCD为2cm．B、C两点在以点A为圆心的