题目内容
如图,在平面直角坐标系xOy中,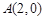 ,
,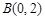 ,⊙C的圆
,⊙C的圆
心为点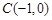 ,半径为1.若D是⊙C上的一个动点,线段
,半径为1.若D是⊙C上的一个动点,线段
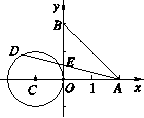
DA与y轴交于点E,则△ABE面积的最大值是
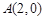 ,
,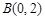 ,⊙C的圆
,⊙C的圆心为点
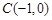 ,半径为1.若D是⊙C上的一个动点,线段
,半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最大值是

| A.2 | B.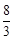 |
C.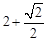 | D.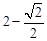 |
C
当⊙C与AD相切时,△ABE面积最大,
连接CD,
则∠CDA=90°,
∵A(2,0),B(0,2),⊙C的圆心为点C(-1,0),半径为1,
∴CD=1,AC=2+1=3,
∴AD= =2
=2 ,
,
∵∠AOE=∠ADC=90°,∠EAO=∠CAD,
∴△AOE∽△ADC,
∴
即 ,∴OE=
,∴OE= ,
,
∴BE=OB+OE=2+
∴S△ABE=
BE?OA= ×(2+
×(2+ )×2=2+
)×2=2+
故答案为C.
连接CD,
则∠CDA=90°,
∵A(2,0),B(0,2),⊙C的圆心为点C(-1,0),半径为1,
∴CD=1,AC=2+1=3,
∴AD=
 =2
=2 ,
,∵∠AOE=∠ADC=90°,∠EAO=∠CAD,
∴△AOE∽△ADC,
∴

即
 ,∴OE=
,∴OE= ,
,∴BE=OB+OE=2+

∴S△ABE=

BE?OA=
 ×(2+
×(2+ )×2=2+
)×2=2+
故答案为C.

练习册系列答案
相关题目
 的切线,切点分别是A、B,若∠APB=60°,PA=4.则⊙⊙的半径是__________.
的切线,切点分别是A、B,若∠APB=60°,PA=4.则⊙⊙的半径是__________.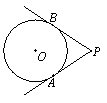

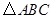 中,
中,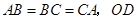 、
、 为
为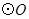 的半径,
的半径,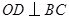 于
于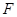 ,
,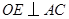 于点
于点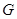 ,求证:
,求证:
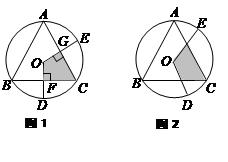
 阴影部分四边形
阴影部分四边形 的面积是
的面积是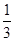 .
.
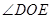 保持
保持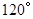 角度不变,求证:当
角度不变,求证:当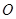 点旋转时,由两条半径
点旋转时,由两条半径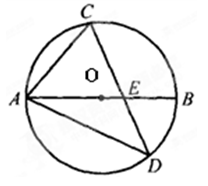
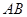 宽为10米,净
宽为10米,净 为7米,则此隧道单心圆的半径
为7米,则此隧道单心圆的半径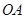 是( )
是( )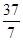
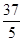
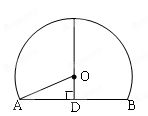
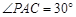 ,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.
,在射线AC上顺次截取AD=3cm,DB=10cm,以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.