题目内容
4.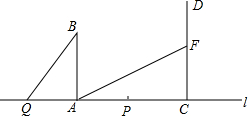 如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4.直线l上有一点C在点P右侧,PC=4cm,过点C作射线CD⊥l,点F为射线CD上的一个动点,连结AF.当△AFC与△ABQ全等时,AQ=12cm.
如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4.直线l上有一点C在点P右侧,PC=4cm,过点C作射线CD⊥l,点F为射线CD上的一个动点,连结AF.当△AFC与△ABQ全等时,AQ=12cm.
分析 根据直角三角形的全等的判定解答即可.
解答 解:要使△AFC与△ABQ全等,
则应满足$\left\{\begin{array}{l}{AB=AC}\\{∠BAQ=∠ACF=90°}\\{AQ=FC}\end{array}\right.$,
∵AQ:AB=3:4,AQ=AP,PC=4cm,
设AQ=3x,AB=4x,则有4x-3x=4,
∴x=4,
∴AQ=12,
故答案为:12.
点评 此题考查直角三角形的全等问题,关键是根据SAS证明三角形的全等.

练习册系列答案
相关题目
19.定理“等腰三角形的两个底角相等”的逆定理是( )
| A. | 有两个角相等的三角形是等腰三角形 | |
| B. | 有两个底角相等的三角形是等腰三角形 | |
| C. | 有两个角不相等的三角形不是等腰三角形 | |
| D. | 不是等腰三角形的两个角不相等 |
9.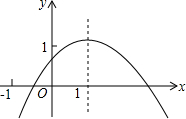 如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a-b>0,
③a+b+c>0,
④a-b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
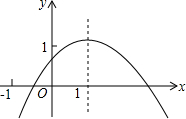 如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:①a<0,b<0,
②2a-b>0,
③a+b+c>0,
④a-b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
| A. | ①②③ | B. | ②③④ | C. | ③④⑤ | D. | ①③④ |
16.用代数式表示a、b两数的和与a、b两数的差的积是( )
| A. | (a+b)(a-b) | B. | (a+b)•a-b | C. | a•(a+b)-b | D. | (a+b)-ab |
13.实数16的平方根是( )
| A. | 4 | B. | ±4 | C. | 2$\sqrt{2}$ | D. | ±2$\sqrt{2}$ |
14.平面直角坐标系中,已知A(8,0),△AOP为等腰三角形且面积为16,满足条件的P点有( )
| A. | 12个 | B. | 10个 | C. | 8个 | D. | 6个 |