题目内容
 已知:如图,在平面直角坐标系xOy中,抛物线y1=ax2+bx过点A(6,0)和点B(3,
已知:如图,在平面直角坐标系xOy中,抛物线y1=ax2+bx过点A(6,0)和点B(3,| 3 |
(1)求抛物线y1的解析式;
(2)将抛物线y1沿x轴翻折得抛物线y2,求抛物线y2的解析式;
(3)在(2)的条件下,抛物线y2上是否存在点M,使△OAM与△AOB相似?如果存在,求出点M的坐标;如果不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)利用待定系数法将A,B两点代入求出即可;
(2)将抛物线y1沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点B′(3 , -
),进而利用待定系数法求出即可;
(3)①当点M在x轴下方时,△OAM就是△OAB';②当点M在x轴上方时,假设△OAM∽△OBA,分别得出M点坐标即可.
(2)将抛物线y1沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点B′(3 , -
| 3 |
(3)①当点M在x轴下方时,△OAM就是△OAB';②当点M在x轴上方时,假设△OAM∽△OBA,分别得出M点坐标即可.
解答:解:(1)依题意,得
解得
,
∴抛物线y1的解析式为:y1=-
x2+
x.
(2)将抛物线y1沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点B′(3 , -
),
设抛物线y2的解析式为:y2=mx2+nx,
∴
,
解得:
∴抛物线y2的解析式为y2=
x2-
x;
(3)过点B作BC⊥x轴于点C,
则有tan∠BOC=
=
.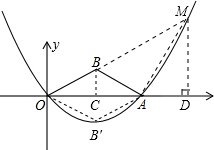
∴∠BOC=30°,∠OBC=60°.
∵OC=3,OA=6,
∴AC=3.
∴∠BAC=30°,∠OBA=120°.
∴OB=AB.
即△OBA是顶角为120°的等腰三角形.
分两种情况:
①当点M在x轴下方时,△OAM就是△OAB',此时点M的坐标为M(3 , -
).
②当点M在x轴上方时,假设△OAM∽△OBA,
则有AM=OA=6,∠OAM=120°.
过点M作MD⊥x轴于点D,则∠MAD=60°.
∴MD=3
,AD=3.∴OD=9.
而(9,3
)满足关系式y2=
x2-
x,
即点M在抛物线y2=
x2-
x上.
根据对称性可知,点(-3 , 3
)也满足条件.
综上所述,点M的坐标为M1(3 , -
),M2(9 , 3
),M3(-3 , 3
).
|
解得
|
∴抛物线y1的解析式为:y1=-
| ||
| 9 |
2
| ||
| 3 |
(2)将抛物线y1沿x轴翻折后,仍过点O(0,0),A(6,0),还过点B关于x轴的对称点B′(3 , -
| 3 |
设抛物线y2的解析式为:y2=mx2+nx,
∴
|
解得:
|
∴抛物线y2的解析式为y2=
| ||
| 9 |
2
| ||
| 3 |
(3)过点B作BC⊥x轴于点C,
则有tan∠BOC=
| BC |
| OC |
| ||
| 3 |

∴∠BOC=30°,∠OBC=60°.
∵OC=3,OA=6,
∴AC=3.
∴∠BAC=30°,∠OBA=120°.
∴OB=AB.
即△OBA是顶角为120°的等腰三角形.
分两种情况:
①当点M在x轴下方时,△OAM就是△OAB',此时点M的坐标为M(3 , -
| 3 |
②当点M在x轴上方时,假设△OAM∽△OBA,
则有AM=OA=6,∠OAM=120°.
过点M作MD⊥x轴于点D,则∠MAD=60°.
∴MD=3
| 3 |
而(9,3
| 3 |
| ||
| 9 |
2
| ||
| 3 |
即点M在抛物线y2=
| ||
| 9 |
2
| ||
| 3 |
根据对称性可知,点(-3 , 3
| 3 |
综上所述,点M的坐标为M1(3 , -
| 3 |
| 3 |
| 3 |
点评:此题主要考查了二次函数综合应用以及相似三角形的性质以及待定系数法求二次函数解析式等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
如果a、b互为相反数,c、d互为倒数,|m-1|=2.那么代数式:2003(a+b)2-4cd+
(a+b)2+6cd+m的值为( )
| 1 |
| 2 |
A、2006
| ||||
| B、4 | ||||
| C、5或1 | ||||
D、2006
|
有下列方程:①
=2;②
=
;③
=
+1;④
=1.其中是分式方程的有( )
| x+1 |
| 3 |
| 2 |
| x-1 |
| 1 |
| x+3 |
| x+2 |
| 3 |
| x-1 |
| 4 |
| 2 |
| x+3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,矩形ABCD中,AB=8,BC=9,点P在BC边上,CP=3,点Q为线段AP上的动点,射线BQ与矩形ABCD的一边交于点R,且AP=BR,则
如图,矩形ABCD中,AB=8,BC=9,点P在BC边上,CP=3,点Q为线段AP上的动点,射线BQ与矩形ABCD的一边交于点R,且AP=BR,则 如图所示,某村庄计划将河水引到水池C中用于农田灌溉,怎样挖渠道最短?请说明理由.
如图所示,某村庄计划将河水引到水池C中用于农田灌溉,怎样挖渠道最短?请说明理由. 如图,AD是圆O的切线,切点为A,AB是圆O的弦.过点B作BC∥AD,交圆O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.判断直线PC与圆O的位置关系,并说明理由.
如图,AD是圆O的切线,切点为A,AB是圆O的弦.过点B作BC∥AD,交圆O于点C,连接AC,过点C作CD∥AB,交AD于点D.连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.判断直线PC与圆O的位置关系,并说明理由. 如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3)
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3)