题目内容
（2013•大庆）如图，三角形ABC是边长为1的正三角形， |
| AB |
|
| AC |
| ||
| 12 |
| ||
| 12 |
分析：设
与
相交于点O，连OA，OB，OC，线段OA将阴影的上方部分分成两个弓形，将这两个弓形分别按顺时针及逆时针方向绕点O旋转120°后，阴影部分便合并成△OBC，得到它的面积等于△ABC面积的三分之一，利用等边三角形的面积公式：
×边长2，即可求得阴影部分的面积．
|
| AB |
|
| AC |
| ||
| 4 |
解答：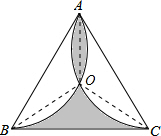
解：如图，设
与
相交于点O，连接OA，OB，OC，线段OA将阴影的上方部分分成两个弓形，将这两个弓形分别按顺时针及反时针绕点O旋转120°后，阴影部分便合并成△OBC，它的面积等于△ABC面积的三分之一，
∴S阴影部分=
×
×12=
．
故答案为：
．
解：如图，设 |
| AB |
|
| AC |
∴S阴影部分=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
故答案为：
| ||
| 12 |
点评：本题考查了旋转的性质：旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段所夹的角等于旋转角．也考查了等边三角形的面积公式：
×边长2．
| ||
| 4 |
练习册系列答案
相关题目
（2013•大庆）如图，已知一次函数y=k1x+b（k1≠0）的图象分别与x轴，y轴交于A，B两点，且与反比例函数y=
（2013•大庆）如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置．F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H．
（2013•大庆）如图，平面直角坐标系中，以点C（2，
（2013•大庆）如图所示，AB是半圆O的直径，AB=8，以AB为一直角边的直角三角形ABC中，∠CAB=30°，AC与半圆交于点D，过点D作BC的垂线DE，垂足为E．