题目内容
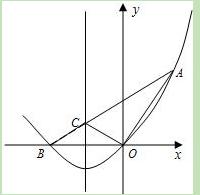
如图,在平面直角坐标系中,点A的坐标为(1,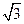 )
) ,△AOB的面积是
,△AOB的面积是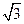 .
.
(1)求点B的坐标;
(2)求过点A、O、B的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(4)在(2)中x轴下方的抛物线上是否存在一点P,过点P作x轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3?若存在,求出点P的坐标;若不存在,请说明理由.
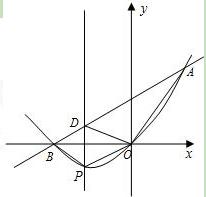
解:(1)由题意得 OB•
OB•  =
= 
∴B(-2,0).
(2)设抛物线的解析式为y=ax(x+2),代入点A(1, ),得
),得 ,
,
∴ ,
,
(3)存在点C、过点A作AF垂直于x轴于点F,抛物线
的对称轴x=-1交x轴于点E、当点C位于对称轴
与线段AB的交点时,△AOC的周长最小,
∵△BCE∽△BAF,∴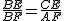 ,
,
∴CE= 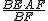 =
=  ,∴C(-1,
,∴C(-1, ).
).
(4)存在、如图,设p(x,y),直线AB为y=kx+b,则 解得
解得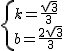 ,
,
∴直线AB为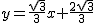 ,S四BPOD=S△BPO+S
,S四BPOD=S△BPO+S △BOD=
△BOD=  |OB||YP|+
|OB||YP|+  |OB||YD|=|YP|+|YD|
|OB||YD|=|YP|+|YD|
=  ,
,
∵S△AOD=S△AOB-S△BOD=  -
-  ×2×|
×2×|  x+
x+ 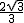 |="-"
|="-"  x+
x+  ,
,
∴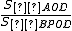 =" ="
=" =" 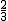 ,
,
∴x1="-"  ,x2=1(舍去),
,x2=1(舍去),
∴p(-  ,-
,- 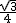 ),
),
又∵S△BOD=  x+
x+ 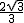 ,
,
∴ =" ="
=" =" 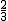 ,
,
∴x1="-"  ,x2=-2.
,x2=-2.
P(-2,0),不符合题意.
∴存在,点P坐标是(-  ,-
,- 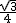 ).
).
解析

练习册系列答案
相关题目
 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD. (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是 如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为
如图,在平面直角坐标中,等腰梯形ABCD的下底在x轴上,且B点坐标为(4,0),D点坐标为(0,3),则AC长为 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.