题目内容
如图,定义:若双曲线
 与它的其中一条对称轴y=x相交于A、B两点,则线段AB称为双曲线
与它的其中一条对称轴y=x相交于A、B两点,则线段AB称为双曲线
 的对径.
的对径.

(1)求双曲线 的对径的长;
的对径的长;
(2)若双曲线
 的对径的长是10
的对径的长是10 ,求k的值;
,求k的值;
(3)仿照上述定义,定义双曲线
 的对径.
的对径.
【答案】
(1) ;(2)
;(2) ;(3)若双曲线
;(3)若双曲线
 与它的其中一条对称轴
与它的其中一条对称轴 相交于A、B两点,则线段AB称为双曲线
相交于A、B两点,则线段AB称为双曲线
 的对径.
的对径.
【解析】
试题分析:(1)过A点作AC⊥x轴于C,解方程组 得到点A、B的坐标,即可得到OC、AC的长,从而求得OA、AB的长,即可求得结果;
得到点A、B的坐标,即可得到OC、AC的长,从而求得OA、AB的长,即可求得结果;
(2)由双曲线的对径为 可得
可得
 ,即得
,即得
 ,从而可以求得点A的坐标,再代入双曲线
,从而可以求得点A的坐标,再代入双曲线
 即可求得结果;
即可求得结果;
(3)根据题意“双曲线
 的对径”的定义求解即可.
的对径”的定义求解即可.
(1)过A点作AC⊥x轴于C

解方程组 得
得 ,
, ,
,
∴A点坐标为 ,B点坐标为
,B点坐标为
∴ ,
,
∴ ,
,
∴ ,
,
∴双曲线 的对径的长是
的对径的长是 ;
;
(2)∵双曲线的对径为 ,即
,即
 ,
,
 ,
,
∴ ,
,
∴ ,
,
∴点A坐标为
把A 代入双曲线
代入双曲线
 得
得 ,
,
即k的值为 ;
;
(3)若双曲线
 与它的其中一条对称轴
与它的其中一条对称轴 相交于A、B两点,
相交于A、B两点,
则线段AB称为双曲线
 的对径.
的对径.
考点:反比例函数的性质
点评:此类问题是初中数学的重点,在中考中比较常见,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
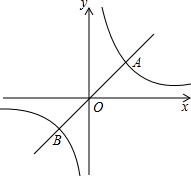 (2012•兰州)如图,定义:若双曲线y=
(2012•兰州)如图,定义:若双曲线y= (k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线
(k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线 的对径.
的对径. ,求k的值.
,求k的值.
 (k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线y=
(k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线y= (k>0)的对径.
(k>0)的对径. 的对径.
的对径. (k>0)的对径是10
(k>0)的对径是10 ,求k的值.
,求k的值. (k<0)的对径.
(k<0)的对径.
 (k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线y=
(k>0)与它的其中一条对称轴y=x相交于A、B两点,则线段AB的长度为双曲线y= (k>0)的对径.
(k>0)的对径. 的对径.
的对径. (k>0)的对径是10
(k>0)的对径是10 ,求k的值.
,求k的值. (k<0)的对径.
(k<0)的对径.