题目内容
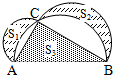 如图,已知Rt△ABC,∠ACB=90°,∠ABC=30°,AB=2,分别以△ABC的三条边为直径作半圆,则图中阴影部分的面积S1、S2、S3之间关系成立的是
如图,已知Rt△ABC,∠ACB=90°,∠ABC=30°,AB=2,分别以△ABC的三条边为直径作半圆,则图中阴影部分的面积S1、S2、S3之间关系成立的是
- A.S1+S2+S3=π
- B.S1+S2=S3
- C.S1+S2>S3
- D.S1+S2<S3
B
分析:连接OC,根据三角形的面积公式,以及扇形的面积公式分别求得S1、S2、S3的值,然后即可判断.
解答: 解:连接OC.
解:连接OC.
∵Rt△ABC,∠ACB=90°,∠ABC=30°,AB=2,
∴AC=1,BC= .
.
以AC为直径的半圆的面积是 π(
π( )2=
)2= π,
π,
以BC为直径的半圆的面积是: π(
π( )2=
)2= π.
π.
则S1= π+S△AOC-扇形OAC=
π+S△AOC-扇形OAC= π+
π+ -
- =
= -
- ,
,
同理,S2= +
+ ,
,
S3= AC•BC=
AC•BC= ×1×
×1× =
= ,
,
则各个选项中只有B正确.
故选B.
点评:本题主要考查了扇形的面积公式,三角形的面积公式,正确求得S1、S2、S3的值是解题的关键.
分析:连接OC,根据三角形的面积公式,以及扇形的面积公式分别求得S1、S2、S3的值,然后即可判断.
解答:
 解:连接OC.
解:连接OC.∵Rt△ABC,∠ACB=90°,∠ABC=30°,AB=2,
∴AC=1,BC=
 .
.以AC为直径的半圆的面积是
 π(
π( )2=
)2= π,
π,以BC为直径的半圆的面积是:
 π(
π( )2=
)2= π.
π.则S1=
 π+S△AOC-扇形OAC=
π+S△AOC-扇形OAC= π+
π+ -
- =
= -
- ,
,同理,S2=
 +
+ ,
,S3=
 AC•BC=
AC•BC= ×1×
×1× =
= ,
,则各个选项中只有B正确.
故选B.
点评:本题主要考查了扇形的面积公式,三角形的面积公式,正确求得S1、S2、S3的值是解题的关键.

练习册系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.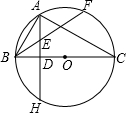 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为