Question

已知BD垂直平分AC，∠BCD=∠ADF，AF⊥AC，

（1）证明四边形ABDF是平行四边形；

（2）若AF=DF=5，AD=6，求AC的长．

Answer 1

【考点】平行四边形的判定；线段垂直平分线的性质；勾股定理．

【分析】（1）先证得△ADB≌△CDB求得∠BCD=∠BAD，从而得到∠ADF=∠BAD，所以AB∥FD，因为BD⊥AC，AF⊥AC，所以AF∥BD，即可证得．

（2）先证得平行四边形是菱形，然后根据勾股定理即可求得．

【解答】（1）证明：∵BD垂直平分AC，

∴AB=BC，AD=DC，

在△ADB与△CDB中，

，

∴△ADB≌△CDB（SSS）

∴∠BCD=∠BAD，

∵∠BCD=∠ADF，

∴∠BAD=∠ADF，

∴AB∥FD，

∵BD⊥AC，AF⊥AC，

∴AF∥BD，

∴四边形ABDF是平行四边形，

（2）解：∵四边形ABDF是平行四边形，AF=DF=5，

∴▱ABDF是菱形，

∴AB=BD=5，

∵AD=6，

设BE=x，则DE=5﹣x，

∴AB²﹣BE²=AD²﹣DE²，

即5²﹣x²=6²﹣（5﹣x）²

解得：x=，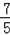

∴=，

∴AC=2AE=．

【点评】本题考查了平行四边形的判定，菱形的判定和性质以及勾股定理的应用．