题目内容
下列命题:
①若b=2a+
c,则一元二次方程ax2+bx+c=0必有一根为-2
②若ac<0,则方程cx2+bx+a=0有两个不等实数根
③若b2-4ac=0,则方程cx2+bx+a=0有两个相等实数根
④二次根式
是一个无理数
其中正确的命题个数是( )
①若b=2a+
| 1 |
| 2 |
②若ac<0,则方程cx2+bx+a=0有两个不等实数根
③若b2-4ac=0,则方程cx2+bx+a=0有两个相等实数根
④二次根式
| x2+9 |
其中正确的命题个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:根与系数的关系,二次根式的定义,根的判别式
专题:
分析:①将b=2a+
c代入方程,利用十字相乘法进行计算;
②利用ac<0和根的判别式进行判断即可;
③根据c=0时可知b=0,此时不是一元二次方程,再分a=0与a≠0进行讨论;
④当x=0时,
=3,依此判断.
| 1 |
| 2 |
②利用ac<0和根的判别式进行判断即可;
③根据c=0时可知b=0,此时不是一元二次方程,再分a=0与a≠0进行讨论;
④当x=0时,
| x2+9 |
解答:解:①将b=2a+
c代入方程得,2ax2+(4a+c)x+2c=0,
即(x+2)(2ax+c)=0,
解得x=-2或x=-
,
必有一根为-2,命题正确;
②cx2+bx+a=O中,△=b2-4ac,
∵ac<0,
∴b2-4ac>0.
故方程cx2+bx+a=O有两个不等实数根,命题正确;
③cx2+bx+a=O中,当c=0时b=0,如果a=0方程有无数个实数根,如果a≠0,方程无实数根,命题错误;
④当x=0时,二次根式
=3,是一个有理数,命题错误.
故选C.
| 1 |
| 2 |
即(x+2)(2ax+c)=0,
解得x=-2或x=-
| c |
| 2a |
必有一根为-2,命题正确;
②cx2+bx+a=O中,△=b2-4ac,
∵ac<0,
∴b2-4ac>0.
故方程cx2+bx+a=O有两个不等实数根,命题正确;
③cx2+bx+a=O中,当c=0时b=0,如果a=0方程有无数个实数根,如果a≠0,方程无实数根,命题错误;
④当x=0时,二次根式
| x2+9 |
故选C.
点评:此题考查了一元二次方程根的判别式、十字相乘法、一元二次方程成立的条件、二次根式的定义等知识,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数轴上的点P到原点的距离为3,点P表示的有理数是( )
| A、3 | B、-3 | C、6 | D、3或-3 |
下列各式中,完全平方公式应用正确的是( )
| A、(2a+3b)2=2a2+12ab+3b2 |
| B、(-x+y)2=-x2+2xy+y2 |
| C、(3a-4b)2=9a2-12ab+16b2 |
| D、(mn-4)2=m2n2-8mn+16 |
若关于x的一元一次方程(3a+2b)x2+ax+b=0有唯一解,则x等于( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
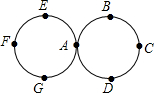 如图,物体从A点出发,按照A→B(第一步)→C(第二步)→D→A→E→F→G→A→B…的顺序循环运动,则第2014步的到达点
如图,物体从A点出发,按照A→B(第一步)→C(第二步)→D→A→E→F→G→A→B…的顺序循环运动,则第2014步的到达点 如图,在△ABC中,AB=10,BC=8,AC=6,AD⊥AB交BC的延长线于D.
如图,在△ABC中,AB=10,BC=8,AC=6,AD⊥AB交BC的延长线于D.