题目内容
在山AB顶上A出测得山CD的山顶C的仰角为30°，然后乘缆车沿线段AC升上山顶C．在点M处，测得山脚D的俯角为45°．如果AB=90米，AM=300米，求山CD的高度．考点：解直角三角形的应用-仰角俯角问题
专题：
分析：作AF⊥CD，ME⊥CD，MN⊥AF，即可求得AB的值，进而可以求得DE的值，根据等腰直角三角形性质即可求得ME的长，即可解题．
解答：解：作AF⊥CD，ME⊥CD，MN⊥AF，
则四边形EFNM为矩形，四边形ABDF为矩形，
∴AB=DF=90米，EF=MN=AM•sin30°=150米，
∴DE=EF+DF=240米，
∵∠DME=45°，
∴DE=ME=240米，
∴CE=ME•tan∠CME=80
，
∴CD=CE+DE=（240+80
）米．
则四边形EFNM为矩形，四边形ABDF为矩形，
∴AB=DF=90米，EF=MN=AM•sin30°=150米，
∴DE=EF+DF=240米，
∵∠DME=45°，
∴DE=ME=240米，
∴CE=ME•tan∠CME=80
| 3 |
∴CD=CE+DE=（240+80
| 3 |
点评：本题考查了直角三角形中三角函数的运用，本题中秋ME的长是解题的关键．
练习册系列答案
相关题目
二次函数y=-
（x+2）2-6的对称轴是（ ）
| 1 |
| 3 |
| A、直线x=-6 | ||
| B、直线x=2 | ||
C、直线x=-
| ||
| D、直线x=-2 |
某市2012年的地方公共财政收入，用四舍五入法取近似值后为27.19亿元，那么这个数值（ ）
| A、精确到亿位 |
| B、精确到百分位 |
| C、精确到千万位 |
| D、精确到百万位 |
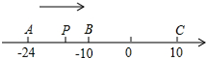已知数轴上有A、B、C三个点，分别表示有理数-24，-10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．