题目内容
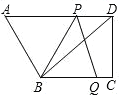
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1,点A、C、D的对应点分别为A1、C1、D1,当点A1落在AC上时.
(1)如图,若∠CAB=60°,求证:四边形ABD1C为平行四边形;
(2)如图,AD1交CB于点O.若∠CAB≠60°,求证:DO=AO.

【答案】(1)见解析;(2)见解析.
【解析】
(1)证△ABA1是等边三角形,得∠AA1B=∠A1BD1,由AC∥BD1,AC=BD1,可得;(2)连接BD1.证△BCD1≌D1A1B,得四边形ABD1C是平行四边形,再证△OCD1≌△OBA(AAS),△DCO≌△ABO(SAS),可得DO=OA.
证明:(1)如图1中,
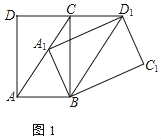
∵∠BAC=60°,BA=BA1,
∴△ABA1是等边三角形,
∴∠AA1B=60°,
∵∠A1BD1=60°,
∴∠AA1B=∠A1BD1,
∴AC∥BD1,
∵AC=BD1,
∴四边形ABD1C是平行四边形.
(2)如图2中,连接BD1.
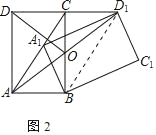
∵∠BCD1=∠BAD1=90°,BD1=D1B,BC=A1D1,
∴△BCD1≌D1A1B,
∴CD1=BA1,
∵BA=BA1,
∴AB=CD1,∵AC=BD1
∴四边形ABD1C是平行四边形,
∴CD1∥AB,CD1=AB,
∠OCD1=∠ABO,
∵∠COD1=∠AOB,
∴△OCD1≌△OBA(AAS),
∴OC=OB,
∵CD=BA,∠DCO=∠ABO,
∴△DCO≌△ABO(SAS),
∴DO=OA.

练习册系列答案
相关题目