题目内容
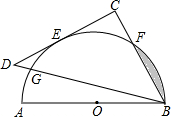（2013•宁波模拟）如图，AB为量角器（半圆O）的直径，等腰直角△BCD的斜边BD交量角器边缘于点G，直角边CD切量角器于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．（1）求量角器在点G处的读数α（0°＜α＜90°）；
（2）若AB=10cm，求阴影部分面积．
分析：如图，连接OE，OF．
（1）利用切线的性质、等腰直角三角形的性质以及平行线的判定证得OE∥BC，则同位角∠ABC=∠AOE=60°，所以由图形中相关角与角间的和差关系即可得到∠ABG=15°；然后由圆周角定理可以求得量角器在点G处的读数α（0°＜α＜90°）；
（2）S阴影=S扇形-S△OBF=
-
．
（1）利用切线的性质、等腰直角三角形的性质以及平行线的判定证得OE∥BC，则同位角∠ABC=∠AOE=60°，所以由图形中相关角与角间的和差关系即可得到∠ABG=15°；然后由圆周角定理可以求得量角器在点G处的读数α（0°＜α＜90°）；
（2）S阴影=S扇形-S△OBF=
| 25π |
| 6 |
25
| ||
| 4 |
解答：
解：如图，连接OE，OF．
（1）∵CD切半圆O于点E，
∴OE⊥CD，
∵BD为等腰直角△BCD的斜边，
∴BC⊥CD，∠D=∠CBD=45°，
∴OE∥BC，
∴∠ABC=∠AOE=60°，
∴∠ABG=∠ABC-∠CBD=60°-45°=15°
∴弧AG的度数=2∠ABG=30°，
∴量角器在点G处的读数α=弧AG的度数=30°；
（2）∵AB=10cm，
∴OF=OB=5cm，∠ABC=60°，
∴△OBF为正三角形，∠BOF=60°，
∴S扇形=
（cm2），S△OBF=
∴S阴影=S扇形-S△OBF=
-
．
解：如图，连接OE，OF．（1）∵CD切半圆O于点E，
∴OE⊥CD，
∵BD为等腰直角△BCD的斜边，
∴BC⊥CD，∠D=∠CBD=45°，
∴OE∥BC，
∴∠ABC=∠AOE=60°，
∴∠ABG=∠ABC-∠CBD=60°-45°=15°
∴弧AG的度数=2∠ABG=30°，
∴量角器在点G处的读数α=弧AG的度数=30°；
（2）∵AB=10cm，
∴OF=OB=5cm，∠ABC=60°，
∴△OBF为正三角形，∠BOF=60°，
∴S扇形=
| 25π |
| 6 |
25
| ||
| 4 |
∴S阴影=S扇形-S△OBF=
| 25π |
| 6 |
25
| ||
| 4 |
点评：本题考查了扇形面积的计算，圆周角定理．求（2）题时，利用了“分割法”求得图中阴影部分的面积．
练习册系列答案
相关题目
（2013•宁波模拟）如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下次沿顺时针方向跳两个点；若停在偶数点上，则下次沿逆时针方向跳一个点．若青蛙从5这点开始跳，则经过2012次后它停在哪个数对应的点上（ ）
（2013•宁波模拟）如图，身高为1.5米的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3米，CA=1米，则树的高度为（ ）
（2013•宁波模拟）如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若圆的半径为r，扇形的圆心角等于120°，则围成的圆锥模型的高为（ ）