题目内容
如图，已知直角三角形的两条直角边长的比为a：b=1：2，其斜边长为4
cm，那么这个三角形的面积是
- A.32cm2
- B.16cm2
- C.8cm2
- D.4cm2
B
分析：设a=x，则b=2x，则根据勾股定理，三条边的长度即可求出，然后利用三角形面积公式即可解答．
解答：设a=x，则b=2x，由勾股定理得：x2+（2x）2=（4）2，解得：x=4
三角形的面积为
x•2x=×4×8=16
故选B．
点评：本题是一道综合性较强的题目，把求三角形的面积和一元二次方程结合起来，锻炼了学生对所学知识的运用能力．
分析：设a=x，则b=2x，则根据勾股定理，三条边的长度即可求出，然后利用三角形面积公式即可解答．
解答：设a=x，则b=2x，由勾股定理得：x2+（2x）2=（4
）2，解得：x=4三角形的面积为
x•2x=×4×8=16故选B．
点评：本题是一道综合性较强的题目，把求三角形的面积和一元二次方程结合起来，锻炼了学生对所学知识的运用能力．
练习册系列答案
相关题目
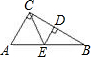如图，已知直角三角形ABC中，∠ACB=90°，E为AB上一点，且CE=EB，ED⊥CB于D，则下列结论中不一定成立的是（ ）| A、AE=BE | ||
B、CE=
| ||
| C、∠CEB=2∠A | ||
D、AC=
|
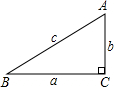如图，已知直角三角形ABC的三边分别为a、b、c，则sinA等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2012•上城区二模）如图，已知直角三角形OAB的直角边OA在x轴上，双曲线y=
如图，已知直角三角形ABC的周长为