��Ŀ����
��ͼ���ھ���ABCD�У�E��AD�ߵ��е㣬BE��AC�ڵ�F������DF�������ĸ����ۣ��١�AEF�ס�CAB����CF��2AF����DF��DC����S�ı���CDEF��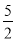 S��ABF.������ȷ�Ľ����У� ����
S��ABF.������ȷ�Ľ����У� ����
��
A. 4�� B. 3�� C. 2�� D. 1��
A ���������������������AE��BC�ɵã���AEF�ס�CBF�����������֪��CBF�ס�CAB�����AEF�ס�CAB�������ȷ���������ƿɵã� ����CF=2AF�������ȷ�����ݽǶ�֮��Ĺ�ϵ���ǿ��Եó���DFC=��DCF���Ӷ��ó�DF=DC��������ȷ���������������εı߳�֮�ȵó���ABF�͡�DFC�ı�ֵ���Ӷ��ó��ı���CDEF�͡�ABF�����֮�ȣ������ȷ���ʱ���ѡA��
��ϰ��ϵ�д�
�����Ŀ
ijУ��һ�Ρ�������ѧ����У�����ʦ���εġ����á������̬�Ƚ��е��飬ͳ���������±���ʾ��
��Ŀ���� | ���� | Ƶ�� |
������Ҫ����ȫ�� | 3 | a |
�ʵ������á��������� | b | 15�� |
Ч�����ã���ȫ���� | c | d |
����ν | e | 2��5�� |
�ϼ� | 40 | 1 |
��1�����ݱ������ݷֱ����a��b��c��d��e��ֵ��
��2�����ݵ�������������ΪӦ�ø���ʦ���һЩ�����Ľ��飿
��1��a=7.5�� b=6 d =75�� c=30 e=1 ��2��������ʦ������Ҫ���á� �����������������Ƶ�ʣ���Ƶ�������������������ݵĸ����ıȡ���֪�༶��������40���������Ƶ��a������b��e,��Ӧ������c��ͨ����������ȥ����������������Ƶ��d.ͨ��������Կ�����ѧ�����Dz�֧�����ã����Խ�����ʦ���������ã���������á��dz���ҪҲ����ʱ������� �����������1��a=3/...��һ������ɲ�����ѡ��У���Ʊ������±���ʾ����Ʊ��Ϊ50����
��ѡ�� | С�� | С�� | С�� | С�� |
��Ʊ��¼ | ��������һ | ���B | �B | ������һ |
��Ʊ�� | 21 | 8 | 2 | 19 |
�ϱ�������ʾ��С�ֵĵ�ƱƵ����_________����ƱƵ��Ϊ_____�� С���ĵ�ƱƵ��_________����ƱƵ��Ϊ_________��
21 0.42 19 0.38 �����������������Ƶ����ָһ�������и��������ظ����ֵĴ�����һ��������ij��ȷ���ķ�Χ�ڳ��ֵ����ݵĸ�����Ƶ�ʣ���Ƶ�������������������ݵĸ����ıȡ� �ӱ����п��Զ�����С�ֵ�ƱƵ��Ϊ21��Ƶ����=0.42��С���ĵ�ƱƵ����19��Ƶ���� =0.38.


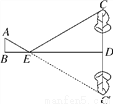
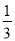 ���ڵ�һ�����ڰ��߶�AB��С��õ��߶�CD�����C������Ϊ�� ��
���ڵ�һ�����ڰ��߶�AB��С��õ��߶�CD�����C������Ϊ�� ��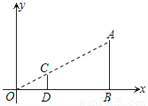
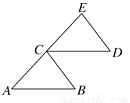
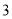 �ĵ�������( )
�ĵ�������( )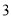 B.
B. 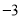 C.
C. 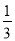 D.
D.