题目内容
已知:在梯形ABCD中,CD∥AB,AD=DC=BC=2,AB=4.点M从A开始,以每秒1个单位的速度向点B运动;点N从点C出发,沿C→D→A方向,以每秒1个单位的速度向点A运动,若M、N同时出发,其中一点到达终点时,另一个点也停止运动.运动时间为t秒,过点N作NQ⊥CD交AC于点Q.

(1)设△AMQ的面积为S,求S与t的函数关系式,并写出t的取值范围.
(2)在梯形ABCD的对称轴上是否存在点P,使△PAD为直角三角形?若存在,求点P到AB的距离;若不存在,说明理由.
(3)在点M、N运动过程中,是否存在t值,使△AMQ为等腰三角形?若存在,求出t值;若不存在,说明理由.
(1) (0<t≤2),
(0<t≤2), (2≤t<4);(2)
(2≤t<4);(2) ;(3)t=
;(3)t= ,12-6
,12-6 ,2.
,2.
【解析】
试题分析:(1)求出t的临界点t=2,分别求出当0<t≤2时和2≤t<4时,S与t的函数关系式即可,
(2)作梯形对称轴交CD于K,交AB于L,分3种情况进行讨论,①取AD的中点G,②以D为直角顶点,③以A为直角顶点,
(3)当0<t≤2时,若△AMQ为等腰三角形,则MA=MQ或者AQ=AM,分别求出t的值,然后判断t是否符合题意.
试题解析:(1)当0<t≤2时,
如图:过点Q作QF⊥AB于F,过点C作CE⊥AB于E,

∵AB∥CD,
∴QF⊥CD,
∵NQ⊥CD,
∴N,Q,F共线,
∴△CQN∽△AFQ,
∴  ,
,
∵CN=t,AF=AE-CN=3-t,
∵NF= ,
,
∴QF= ,
,
∴ ,
,
∴ ,
,
当2≤t<4时,
如图:△FQC∽△PQA,
∵DN=t-2,
∴FD=DN•cos∠FDN=DN•cos60°= (t-2),
(t-2),
∴FC=CD+FD=2+ (t-2)=
(t-2)= ,
,
∴FQ=FC•tan∠FCQ=FC•tan30°=( )•
)• =
= (t+2),
(t+2),
∴PQ=PF-FQ= ,
,

∴ ;
;
(2)作梯形对称轴交CD于K,交AB于L,
情况一:取AD的中点G,GD=1,
过G作GH⊥对称轴于H,GH=1.5,
∵1.5>1,
∴以P为直角顶点的Rt△PAD不存在,
情况二:以D为直角顶点:KP1= ,
,
∴P1L= ,
,
情况三:以A为直角顶点,LP2= ,
,
综上:P到AB的距离为 时,△PAD为Rt△,
时,△PAD为Rt△,
(3)0<t≤2时, 若MA=MQ,
则: =
= ,
,
∴t= ,
,
若AQ=AM,则t= ,
,
解得t=12-6 ,
,
若QA=QM,则∠QMA=30°
而0<t≤2时,∠QMA>90°,
∴QA=QM不存在;
2≤t<4(图中)
若QA=QM,AP:AD= :2,
:2,
∴t=2,
若AQ=AM,2 -
- (t+2)=t,
(t+2)=t,
∴t=2 -2,
-2,
∵2 -2<2,
-2<2,
∴此情况不存在若MA=MQ,则∠AQM=30°,而∠AQM>60°不存在.
综上:t= ,12-6
,12-6 ,2时,△AMQ是等腰三角形.
,2时,△AMQ是等腰三角形.
考点: 1.等腰梯形的性质;2.等腰三角形的判定;3.直角三角形的性质.

 名校课堂系列答案
名校课堂系列答案 已知:在梯形ABCD中,AD∥BC,点E在AB上,点F在DC上,且AD=a,BC=b.
已知:在梯形ABCD中,AD∥BC,点E在AB上,点F在DC上,且AD=a,BC=b.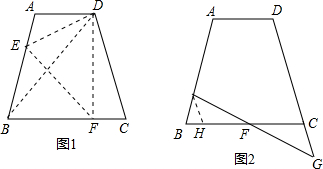
 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长? 已知:在梯形ABCD中,AD∥BC,AB=DC=5,AD=3.5,
已知:在梯形ABCD中,AD∥BC,AB=DC=5,AD=3.5, 已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E、F分别是BC和DC的中点,连接AE、EF和BD,AE和BD相交于点G.
已知,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E、F分别是BC和DC的中点,连接AE、EF和BD,AE和BD相交于点G.