题目内容
3.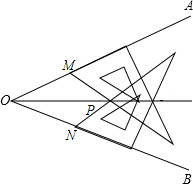 已知:小明在∠AOB的两边上分别取点M,N,使得OM=ON,并把两个完全一样的含有30°的直角三角板按如图所示的位置进行放置,两个直角三角板的斜边交于点P.小明说:“射线OP是∠AOB的平分线”.
已知:小明在∠AOB的两边上分别取点M,N,使得OM=ON,并把两个完全一样的含有30°的直角三角板按如图所示的位置进行放置,两个直角三角板的斜边交于点P.小明说:“射线OP是∠AOB的平分线”.请问:小明的说法正确吗?若正确,请给出证明,若不正确,请说明理由.
分析 过O点作OC⊥PM于C,OD⊥PN于D,求出△OMC≌△OND,根据全等三角形的性质得出OC=OD,∠COM=∠DON,根据角平分线性质求出∠CPO=∠DPO.根据三角形外角的行中性质求出即可.
解答 解:正确;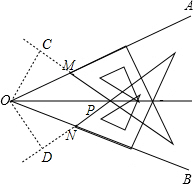 过O点作OC⊥PM于C,OD⊥PN于D.
过O点作OC⊥PM于C,OD⊥PN于D.
∴∠C=∠D=90°,
由题意,∠PMA=∠PNB=60°,
∴∠OMC=∠PMA=60°,∠OND=∠PNB=60°.
∴∠OMC=∠OND.
在△OMC和△OND中,
$\left\{\begin{array}{l}{∠CMO=∠DNO}\\{∠OCM=∠ODN=90°}\\{OM=ON}\end{array}\right.$,
∴△OMC≌△OND(AAS),
∴OC=OD,∠COM=∠DON,
∵OC⊥PM于C,OD⊥PN于D,
∴点O在∠CPD的平分线上,
∴∠CPO=∠DPO,
∴∠COP=∠DOP,
∴∠MOP=∠NOP,
即:射线OP是∠AOB的平分线.
点评 本题考查了角平分线的判定和全等三角形的判定和性质的应用,关键是正确作出辅助线,掌握全等三角形的判定方法.

练习册系列答案
相关题目
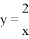 过两点(﹣1,
过两点(﹣1,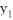 ),(﹣3,
),(﹣3,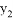 ),则
),则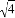 ×(2017-π)0+(
×(2017-π)0+( )-2
)-2
 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( )
ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( )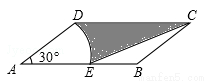
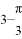 B.
B. 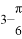 C.
C. 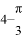 D.
D. 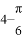
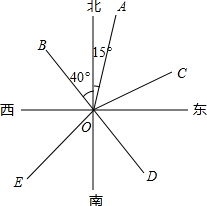 如图,OA的方向是北偏东15°,OB的方向是北偏西40°.
如图,OA的方向是北偏东15°,OB的方向是北偏西40°. 根据几何体的三视图,画出它的展开图.
根据几何体的三视图,画出它的展开图.