题目内容
为执行“两免一补”政策,某地区2013年投入教育经费3600万元,预计2015年投入4900万元.设这两年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )
| A、3600x2=4900 |
| B、3600(1+x)2=4900 |
| C、3600(1+x%)2=4900 |
| D、3600(1+x)2+3600(1+x)=4900 |
考点:由实际问题抽象出一元二次方程
专题:增长率问题
分析:利用增长后的量=增长前的量×(1+增长率),如果设这两年投入教育经费的年平均增长百分率为x,然后用x表示2014年的投入,再根据“2015年投入4900万元”可得出方程.
解答:解:设这两年投入教育经费的年平均增长百分率为x,由题意得
3600(1+x)2=4900.
故选:B.
3600(1+x)2=4900.
故选:B.
点评:此题考查从实际问题中抽象出一元二次方程,平均增长率问题,一般形式为a(1+x)2=b,a为起始时间的有关数量,b为终止时间的有关数量.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
本学期的五次数学测试中,甲、乙两同学的平均成绩一样,方差分别为1.3、0.4,由此可知( )
| A、甲比乙的成绩稳定 |
| B、乙比甲的成绩稳定 |
| C、甲乙两人的成绩一样稳定 |
| D、无法确定谁的成绩更稳定 |
函数y=kx-k与y=kx2的图象大致是( )
A、 |
B、 |
C、 |
D、 |
一个角的两边与另一个角的两边分别平行,那么这两个角( )
| A、相等 | B、互补 |
| C、相等或互补 | D、不能确定 |
下列方程组是二元一次方程组的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
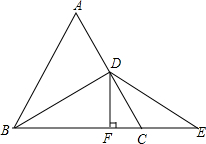 如图,BD是等边三角形ABC的角平分线,E是BC延长线上的一点,且CE=CD,DF⊥BC,垂足为F.BF与EF相等吗?为什么?
如图,BD是等边三角形ABC的角平分线,E是BC延长线上的一点,且CE=CD,DF⊥BC,垂足为F.BF与EF相等吗?为什么?