题目内容
已知∠AOB=40°,过点O引射线OC,若∠AOC:∠COB=2:3,且OD平分∠AOB.则∠COD=________.
4°或100°
分析:分射线OC在∠AOB的内部、射线OC在∠AOB的外部两种情况进行解答,当射线OC在∠AOB的内部时,设∠AOC、∠COB的度数分别为2x、3x,计算出x的值,进而计算出∠AOC、∠AOD的度数,从而得出结论.当射线OC在∠AOB的外部时,∠AOC、∠COB的度数分别为2x、3x,则∠AOB=x,得x的值,进而计算出∠AOC与∠AOD的度数,然后得出结论.
解答:如图(1)射线OC在∠AOB的内部,(2)射线OC在∠AOB的外部

(1)设∠AOC、∠COB的度数分别为2x、3x,则2x+3x=40°
∴x=8°,∠AOC=2x=16°,∠AOD= ×40°=20°
×40°=20°
∴∠COD=∠AOD-∠AOC=20°-16°=4°;
(2)设∠AOC、∠COB的度数分别为2x、3x,则∠AOB=3x-2x=x=40°,
∴∠AOC=2x=80°
∠AOD=20°
∴∠COD=∠AOC+∠AOD=80°+20°=100°.
故答案为4°或100°.
点评:本题分射线OC在∠AOB的内部、射线OC在∠AOB的外部两种情况,不能漏解.
分析:分射线OC在∠AOB的内部、射线OC在∠AOB的外部两种情况进行解答,当射线OC在∠AOB的内部时,设∠AOC、∠COB的度数分别为2x、3x,计算出x的值,进而计算出∠AOC、∠AOD的度数,从而得出结论.当射线OC在∠AOB的外部时,∠AOC、∠COB的度数分别为2x、3x,则∠AOB=x,得x的值,进而计算出∠AOC与∠AOD的度数,然后得出结论.
解答:如图(1)射线OC在∠AOB的内部,(2)射线OC在∠AOB的外部

(1)设∠AOC、∠COB的度数分别为2x、3x,则2x+3x=40°
∴x=8°,∠AOC=2x=16°,∠AOD=
 ×40°=20°
×40°=20°∴∠COD=∠AOD-∠AOC=20°-16°=4°;
(2)设∠AOC、∠COB的度数分别为2x、3x,则∠AOB=3x-2x=x=40°,
∴∠AOC=2x=80°
∠AOD=20°
∴∠COD=∠AOC+∠AOD=80°+20°=100°.
故答案为4°或100°.
点评:本题分射线OC在∠AOB的内部、射线OC在∠AOB的外部两种情况,不能漏解.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
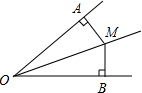 如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MAB等于( )
如图,已知∠AOB=40°,OM平分∠AOB,MA⊥OA,MB⊥OB,垂足分别为A、B两点,则∠MAB等于( )| A、50° | B、40° | C、30° | D、20° |
 9、如图,已知∠AOB=40°,∠AOC=Rt∠,OD平分∠BOC,则∠AOD的度数是( )
9、如图,已知∠AOB=40°,∠AOC=Rt∠,OD平分∠BOC,则∠AOD的度数是( ) 14、如图,已知∠AOB=40°,∠AOC=Rt∠,OD平分∠BOC,则∠AOD的度数是
14、如图,已知∠AOB=40°,∠AOC=Rt∠,OD平分∠BOC,则∠AOD的度数是 (1)如图,已知∠AOB=40°,P为OB上的一点,在∠AOB内,求作一个以OP为底边,底角为20°的等腰三角形OCP(尺规作图,要求保留作图痕迹,不必写出作法).
(1)如图,已知∠AOB=40°,P为OB上的一点,在∠AOB内,求作一个以OP为底边,底角为20°的等腰三角形OCP(尺规作图,要求保留作图痕迹,不必写出作法). 如图,△OAB绕点O逆时针旋转82°到△OCD的位置,已知∠AOB=40°,则∠AOD等于
如图,△OAB绕点O逆时针旋转82°到△OCD的位置,已知∠AOB=40°,则∠AOD等于