题目内容

3．两个三角形具备下列（　　）条件，则它们一定全等．
A．两边和其中一边的对角对应相等B．三个角对应相等
C．两角和一组对应边相等D．两边及第三边上的高对应相等

分析 根据全等三角形的判定定理SSS、SAS、ASA、AAS、HL进行分析，AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．

解答 解：A、两边和其中一边的对角对应相等，不能判定两个三角形全等，故此选项错误；
B、三个角对应相等，不能判定两个三角形全等，故此选项错误；
C、两角和一组对应边相等，可以利用AAS判定两个三角形全等，故此选项正确；
D、两边及第三边上的高对应相等，这两边的夹角有可能一个是锐角一个是钝角，所以这两个三角形不一定全等，故此选项错误；
故选：C．

点评 此题主要考查了全等三角形的判定，关键是掌握判定定理．

练习册系列答案
相关题目
13．乌镇是著名的水乡，如图，圆拱桥的拱顶到水面的距离CD为8m，水面宽AB为8m，则桥拱半径OC为（　　）
A．4mB．5mC．6mD．8m
14．下列方程的变形，符合等式性质的是（　　）
A．由x+2=4，得x=4-2B．由x-3=5，得x=5-3C．由$\frac{1}{2}$x=0，得x=2D．-3x=$\frac{3}{2}$，得x=-$\frac{9}{2}$
11．下列代数式中单项式共有（　　）
$\frac{{x}^{2}-3}{5}$，-xy2，-0.5，$\frac{a}{3}$，$\frac{1}{x-y}$，ax2+bx+c，a2b3，$\frac{ab}{5}$．
A．2个B．3个C．4个D．5个
18．当a=2.7，b=-3.2，c=-1.8时，则-a-b-c=2.3．
8．根据学校合唱比赛的活动细则，每个参赛的合唱团在比赛时须演唱4首歌曲，九（2）班合唱团已确定了2首歌曲，还需在A，B两首歌曲中确定一首，在C、D、E三首歌曲中确定另一首，则确定的参赛歌曲中有一首是D的概率是（　　）
A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$
15．课间操时，小华、小军、小刚的位置如图，如果小华的位置用（0，0）表示，小军的位置用（2，1）表示，那么小刚的位置可以表示成（　　）
A．（4，3）B．（4，5）C．（3，4）D．（5，4）
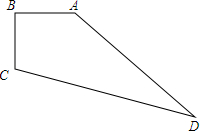12．如图，在四边形地块ABCD中，∠B=90°，AB=30m，BC=40m，CD=130m，AD=120m，求这块地的面积．
13．已知x-2y=6，则3（x-2y）2-5（-x+2y）+6的值为（　　）
A．84B．144C．72D．360

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网