题目内容
18.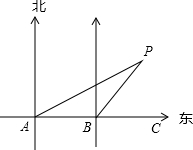 海滨城市某校九(2)班张华(图5中的A处)与李力(图中的B处)两同学在东西方向的沿海路上,分别测得海中灯塔P的方向角为北偏东60°、北偏东30°,此时他们相距800米.
海滨城市某校九(2)班张华(图5中的A处)与李力(图中的B处)两同学在东西方向的沿海路上,分别测得海中灯塔P的方向角为北偏东60°、北偏东30°,此时他们相距800米.(1)∠PBC=60°.
(2)求灯塔P到沿海路的距离(结果用根号表示)
分析 (1)由余角的定义可以求出结论;
(2)在图中两个直角三角形中,先根据已知角的正切函数,分别求出AC和BC,根据它们之间的关系,构建方程解答.
解答  解:(1)∵P在北偏东30°,
解:(1)∵P在北偏东30°,
∴∠PBC=90°-30°=60°,
故答案为:60;
(2)过P作PC⊥AC于C,
由已知得,
在Rt△PBC中,∠PBC=60°,PC=BCtan60°=$\sqrt{3}$BC.
在Rt△APC中,∠PAC=30°,AC=$\sqrt{3}$PC=$\sqrt{3}$×$\sqrt{3}$BC=3BC=800+BC.
解得,BC=400.
∴PC=400$\sqrt{3}$(m).
答:灯塔P到沿海路的距离是400$\sqrt{3}$m.
点评 此题考查的知识点是解直角三角形的应用,关键明确解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
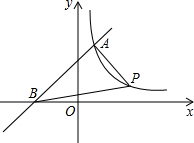 如图,一次函数y=x+3与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(m,4),与x轴相交于点B.
如图,一次函数y=x+3与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(m,4),与x轴相交于点B.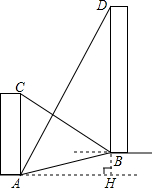 如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是$1:2\sqrt{3}$.从点A测得楼BD顶部D处的仰角是60°,从点B测得楼AC顶部C处的仰角是30°,楼BD的自身高度比楼AC高12m.求楼AC与楼BD之间的水平距离.(结果保留根号)
如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是$1:2\sqrt{3}$.从点A测得楼BD顶部D处的仰角是60°,从点B测得楼AC顶部C处的仰角是30°,楼BD的自身高度比楼AC高12m.求楼AC与楼BD之间的水平距离.(结果保留根号)