Question

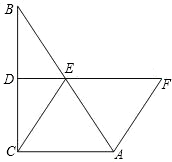
Rt△ABC中，∠ACB=90°，AC=8，BC=6，D是AB中点，E为CB上动点（不与C重合），⊙O是过C、D、E三点的圆．
（1）当E、B重合时，在图1中作出⊙O；
（2）当点E在CB上运动时，求证：∠DFE=∠B，并求出EF的最小值；
（3）在整个过程中求CF的取值范围．

Answer 1

解：（1）如图，⊙O即为所求作的圆．

（2）①证明：∵D是Rt△ABC的中点，
∴DC=DB，即∠DCB=∠B；
∵∠DCB=∠DFE，
∴∠DFE=∠B；
②过D作直径DG，连接CG；
在Rt△DCG中，DG≥CD；
由于EF=DG，故EF≥CD，所以EF最小时，EF=CD，
在Rt△ABC中，AC=8，BC=6，易求得AB=10，则CD=AB=5，
即EF的最小值为5．

（3）如（1）题图，连接DF；
由圆周角定理知：∠BDF=90°，
则△ADF∽△ACB；
∴，即，
∴AF=，CF=8-=；
作CD的垂直平分线直线l，交AC于点M；
连接DM，则CM=DM；
∴∠DCM=∠CDM=∠A；
∴△CDA∽△CMD，
∴CM=CD²÷CA=；
由于OC＜CM，即EF＜2CM=；
由于随着E点的向上运动，CF的值逐渐增大，因此CF的取值范围为：
≤CF＜．
分析：（1）当E、B重合时，⊙O经过C、D、B三点，分别作CD、BD、CB中任意两边的垂直平分线，垂直平分线的交点即为圆心O，然后以OB为半径作圆即可．
（2）由于D是斜边AB的中点，所以CD=BD，即∠DCB=∠B，联立由圆周角得到的∠DFE=∠DCB即可得证；过D作直径DG，连接CG，在Rt△DCG中，直径DG（即EF）≥CD，因此当EF最小时，EF=CD，由此求得EF的最小值．
（3）由与O是△CDE三边中垂线的交点，因此点O在CD的垂直平分线上运动，设CD中垂线与AC交于M，当E点向上运动时，CE的垂直平分线与CD垂直平分线的交点O无限接近M点，因此此题应考虑两种情况：
①E、B重合时，此时CF值最小，由圆周角定理知DF⊥AB，易证得△ADF∽△ACB，根据相似三角形得到的比例线段即可求得AF的长，进而可求得CF的值．
②求CM的长，连接DM，由于M在CD的中垂线上，所以CM=DM，即∠DCM=∠MDC=∠A，由此可证得△CDM∽△CDA，即可求得CM的值；
综合上述两种情况，那么CF的取值范围应该是：大于等于①中CF的值，而小于②的2CM的长．
点评：此题考查了圆周角定理、勾股定理、直角三角形的性质、相似三角形的判定和性质等知识，综合性较强，难度较大．