题目内容
化简求值
-
÷
,其中x=
.
| 1 |
| x+1 |
| x+3 |
| x2-1 |
| x2+4x+3 |
| x2-2x+1 |
| 1 | ||
|
考点:分式的化简求值
专题:
分析:首先把除法转化为乘法,把分式的分子和分母分解因式,计算乘法,然后通分,进行加减即可化简,然后把x的值化简,代入求值即可.
解答:解:原式=
-
•
=
-
=
=
,
当x=
=
-1时,原式=
=2.
| 1 |
| x+1 |
| x+3 |
| (x+1)(x-1) |
| (x-1)2 |
| (x+1)(x+3) |
=
| 1 |
| x+1 |
| x-1 |
| (x+1)2 |
=
| x+1-x+1 |
| (x+1)2 |
=
| 2 |
| (x+1)2 |
当x=
| 1 | ||
|
| 2 |
| 2 | ||
(
|
点评:本题考查了分式的化简求值,分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
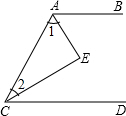 如图,AE平分∠BAC,CE平分∠ACD,且AB∥CD,则∠AEC等于( )
如图,AE平分∠BAC,CE平分∠ACD,且AB∥CD,则∠AEC等于( )| A、60° | B、80° |
| C、100° | D、90° |
若式子
有意义,则x的取值范围为( )
| ||
| x-3 |
| A、x≥2 |
| B、x≠3 |
| C、x≤2或x≠3 |
| D、x≥2且x≠3 |
 如图是写有字的正方体的展开图,则人字的对面写着( )
如图是写有字的正方体的展开图,则人字的对面写着( )| A、知 | B、识 | C、亮 | D、生 |
 如图,正方形ABCD的边长为1,E、F、G、H分别在AD,AB,BC,CD上,且AF=BG=CH=DE=x,当x为何值时,四边形EFGH的面积最小?
如图,正方形ABCD的边长为1,E、F、G、H分别在AD,AB,BC,CD上,且AF=BG=CH=DE=x,当x为何值时,四边形EFGH的面积最小? 如图,在平面直角坐标系xOy中,点A(-2,0),B(-1,-2),C、D在反比例函数y=
如图,在平面直角坐标系xOy中,点A(-2,0),B(-1,-2),C、D在反比例函数y=