Question

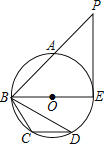
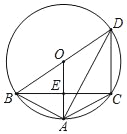
【题目】如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，CD=6，OA交BC于点E，则AE的长度是_____．

Answer 1

【答案】3

【解析】

由已知可证∠BDA=30°；根据BD为⊙O的直径，可证∠BCD=90°，然后利用等边三角形和中位线性质即可求．

∵△ABC内接于⊙O，∠BAC=120°，AB=AC，
∴∠CBA=∠BCA=30°．
∴∠BDA=∠ACB=30°．
∵BD为⊙O的直径，
∴∠BCD=90°，∠BDA=30°，
∴∠BOA=2∠BDA =60°，

∴∠OBC=∠BOA-∠BCA=60°-30°=30°,

∵OB、OA为⊙O的半径，

∴△OAB为等边三角形，

∵∠OBC=∠CBA=30°

∴E是OA中点，BC⊥OA,

∵∠BCD=90°,

∴OA∥CD,

∵∠BAC=120°，AB=AC, BC⊥OA,

∴E是BC中点,

∵O是BD中点

∴，

∴AE=OE=3.