题目内容
△ABC中，∠C=90°，BC=6，AC=8，以C为圆心，以6为半径的圆与直线AB的位置关系是
- A.相切
- B.相交
- C.相离
- D.不能确定
B
分析：判断圆与直线AB边的位置关系，关键是比较点C到直线AB的距离与半径的大小关系．
解答：
解：过C点作CD⊥AB，垂足为D，
∵∠C=90°，BC=6，AC=8，
由勾股定理，得AB=
=10，
根据三角形计算面积的方法可知，BC×AC=AB×CD，
∴CD=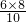
=4.8＜6，
∴⊙C与直线AB相交．
故选B．
点评：本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．
分析：判断圆与直线AB边的位置关系，关键是比较点C到直线AB的距离与半径的大小关系．
解答：
解：过C点作CD⊥AB，垂足为D，∵∠C=90°，BC=6，AC=8，
由勾股定理，得AB=
=10，根据三角形计算面积的方法可知，BC×AC=AB×CD，
∴CD=
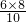=4.8＜6，∴⊙C与直线AB相交．
故选B．
点评：本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
如图，在△ABC中，AC=2，AB=3，D是AC上一点，E是AB上一点，且∠ADE=∠B，设AD=x，AE=y，则y与x之间的函数关系式是（ ）A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
如图，在△ABC中，AB=8，AC=6，BC=7，点D在AC上，AD=2，