题目内容
△ABC中AB=12,AC=8,P是BC上一点且BP=2PC,设Q是△ABC某边一点,若PQ截得三角形与原三角形相似,面积比为1:4,则AQ的长是多少?
考点:相似三角形的性质
专题:
分析:由于Q是△ABC某边一点,所以Q可能在AC边上,也可能在AB边上.①当Q在AC边上时,作BG⊥AC于G,PF⊥AC于F.根据三角形的面积公式得出S△QPC=
QC•PF,S△ABC=
AC•BG,由
=
,得出
=
,根据平行线分线段成比例定理得到
=
=
,于是
•
=
,求出QC=6,那么AQ=AC-QC=8-6=2;②当Q在AB边上时,作PE⊥AB于E,CF⊥AB于F.根据三角形的面积公式得出S△BQP=
BQ•PE,S△ABC=
AB•CF,由
=
,得出
=
,根据平行线分线段成比例定理得到
=
=
,于是
•
=
,求出BQ=
,那么AQ=AB-BQ=12-
=
.
| 1 |
| 2 |
| 1 |
| 2 |
| S△QPC |
| S△ABC |
| 1 |
| 4 |
| QC•PF |
| AC•BG |
| 1 |
| 4 |
| PF |
| BG |
| PC |
| BC |
| 1 |
| 3 |
| QC |
| 8 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| S△BPQ |
| S△ABC |
| 1 |
| 4 |
| BQ•PE |
| AB•CF |
| 1 |
| 4 |
| PE |
| CF |
| BP |
| BC |
| 2 |
| 3 |
| BQ |
| 12 |
| 2 |
| 3 |
| 1 |
| 4 |
| 9 |
| 2 |
| 9 |
| 2 |
| 15 |
| 2 |
解答: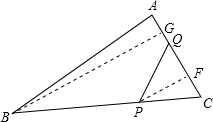 解:分两种情况:
解:分两种情况:
①Q在AC边上时,作BG⊥AC于G,PF⊥AC于F.S△QPC=
QC•PF,S△ABC=
AC•BG,
∵
=
,
∴
=
,
∵PF∥BG,
∴
=
=
,
∴
•
=
,
∴QC=6,
∴AQ=AC-QC=8-6=2;
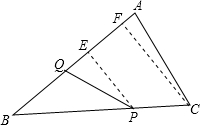 ②Q在AB边上时,作PE⊥AB于E,CF⊥AB于F.S△BQP=
②Q在AB边上时,作PE⊥AB于E,CF⊥AB于F.S△BQP=
BQ•PE,S△ABC=
AB•CF,
∵
=
,
∴
=
,
∵PE∥CF,
∴
=
=
,
∴
•
=
,
∴BQ=
,
∴AQ=AB-BQ=12-
=
;
综上所述,AQ的长为2或
.
 解:分两种情况:
解:分两种情况:①Q在AC边上时,作BG⊥AC于G,PF⊥AC于F.S△QPC=
| 1 |
| 2 |
| 1 |
| 2 |
∵
| S△QPC |
| S△ABC |
| 1 |
| 4 |
∴
| QC•PF |
| AC•BG |
| 1 |
| 4 |
∵PF∥BG,
∴
| PF |
| BG |
| PC |
| BC |
| 1 |
| 3 |
∴
| QC |
| 8 |
| 1 |
| 3 |
| 1 |
| 4 |
∴QC=6,
∴AQ=AC-QC=8-6=2;
 ②Q在AB边上时,作PE⊥AB于E,CF⊥AB于F.S△BQP=
②Q在AB边上时,作PE⊥AB于E,CF⊥AB于F.S△BQP=| 1 |
| 2 |
| 1 |
| 2 |
∵
| S△BPQ |
| S△ABC |
| 1 |
| 4 |
∴
| BQ•PE |
| AB•CF |
| 1 |
| 4 |
∵PE∥CF,
∴
| PE |
| CF |
| BP |
| BC |
| 2 |
| 3 |
∴
| BQ |
| 12 |
| 2 |
| 3 |
| 1 |
| 4 |
∴BQ=
| 9 |
| 2 |
∴AQ=AB-BQ=12-
| 9 |
| 2 |
| 15 |
| 2 |
综上所述,AQ的长为2或
| 15 |
| 2 |
点评:本题考查了三角形的面积,平行线分线段成比例定理,进行分类讨论是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图,是由四个小正方体摆成了立体图,从上往下看到的图是( )
如图,是由四个小正方体摆成了立体图,从上往下看到的图是( )A、 |
B、 |
C、 |
D、 |
在平面直角坐标系中,点A(-2,-3)关于x轴对称点A′在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的三视图不变的情况下,该正方体最多还能放
如图,是由10个完全相同的小正方体堆成的几何体.若现在你还有若干个相同的小正方体,在保证该几何体的三视图不变的情况下,该正方体最多还能放 如图所示,△ABC中,AC=BC,以BC为直径作⊙O交AB于点D,交AC于点G,作直线DF⊥AC交AC于点F,交CB的延长线于点E.
如图所示,△ABC中,AC=BC,以BC为直径作⊙O交AB于点D,交AC于点G,作直线DF⊥AC交AC于点F,交CB的延长线于点E. 如图,直线l与⊙O相离,OA⊥l于点A,交⊙O于点B,点C是⊙O上一点,连接CB并延长交直线l于点D,使AC=AD.
如图,直线l与⊙O相离,OA⊥l于点A,交⊙O于点B,点C是⊙O上一点,连接CB并延长交直线l于点D,使AC=AD.