Question

【题目】如图，有一直径是米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，则：

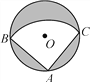
(1)AB的长为多少米？

(2)用该扇形铁皮围成一个圆锥，所得圆锥的底面半径为多少米？

Answer 1

【答案】（1）1米（2）米

【解析】

（1）如下图，连接BC，则由已知易得△ABC是等腰直角三角形，且BC=，∠A=90°，由此可得AB=1；

（2）由AB=1，∠A=90°可得的长度，而由的长度是所围圆锥的底面圆的周长即可计算出底面圆的半径.

（1）如下图，连接BC，

∵在☉O中，∠A=90°，

∴BC是☉O的直径，

∴BC=，

又∵AB=AC，

∴AB=1（米）；

（2）∵AB=1，∠A=90°，

∴，

设扇形ABC围成的圆锥的底面圆的半径为r，则：

，解得：（米）.