题目内容
直线y=x+b与x轴交于A点，与y轴交于B点，若坐标原点O到直线AB的距离为
，则b的值为________．
±4
分析：根据题意可得，函数与x、y轴的交点分别为（-b，0），（0，b），判断出△ABC为等腰直角三角形，再作出O到直线AB的距离，解答即可．
解答：
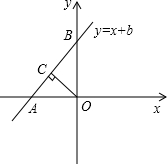解：如图，函数与x、y轴的交点分别为（-b，0），（0，b），
∴∠BAO=∠ABO=45°，
∴
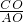=cos45°，
∴AO•cos45°=2
，
∴AO=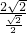
=4，
即b=±4．
故答案为±4．
点评：本题考查了一次函数的性质与等腰直角三角形的性质，熟悉直角三角形的性质是解题的关键．
分析：根据题意可得，函数与x、y轴的交点分别为（-b，0），（0，b），判断出△ABC为等腰直角三角形，再作出O到直线AB的距离，解答即可．
解答：
解：如图，函数与x、y轴的交点分别为（-b，0），（0，b），∴∠BAO=∠ABO=45°，
∴
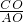=cos45°，∴AO•cos45°=2
，∴AO=
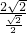=4，即b=±4．
故答案为±4．
点评：本题考查了一次函数的性质与等腰直角三角形的性质，熟悉直角三角形的性质是解题的关键．
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
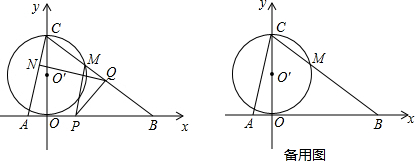
（2012•兰州）如图，M为双曲线y=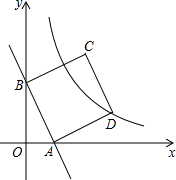
（2013•宛城区一模）如图，直线y=-2x+2与x轴y轴分别相交于点A、B，四边形ABCD是正方形，曲线y=