题目内容
12.(1)25-9+(-12)-(-7);(2)$\frac{1}{9}$×(-2)3÷($\frac{2}{3}$)2;
(3)24×($\frac{2}{3}$-$\frac{5}{6}$-$\frac{3}{8}$)-|$\frac{5}{2}$-1|;
(4)-9×(-$\frac{1}{2}$+$\frac{7}{6}$)-8÷(-2)2+1$\frac{1}{5}$×(-3$\frac{1}{3}$)
(5)解方程:5(x-6)=-4x-3;
(6)解方程:$\frac{2x+1}{3}$=1+$\frac{1-10x}{6}$.
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算即可得到结果;
(3)原式利用乘法分配律,以及绝对值的代数意义计算即可得到结果;
(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(5)方程去括号,移项合并,把x系数化为1,即可求出解;
(6)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)原式=25+7-9-12=32-21=11;
(2)原式=-$\frac{1}{9}$×8×$\frac{9}{4}$=-2;
(3)原式=16-20-9-$\frac{3}{2}$=-14$\frac{1}{2}$;
(4)原式=-6-2-4=-12;
(5)方程去括号得:5x-30=-4x-3,
移项合并得:9x=27,
解得:x=3;
(6)去分母得:4x+2=6+1-10x,
移项合并得:14x=5,
解得:x=$\frac{5}{14}$.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
3.下列等式成立的是( )
| A. | (-a)2=a2 | B. | a+a=a2 | C. | -2+3=-1 | D. | 3a+5b=8ab |
20.下列计算正确的是( )
| A. | 3a+b=3ab | B. | -a2b+2a2b=a2b | C. | 2a3+3a2=5a3 | D. | 3a-a=2 |
7.若|a-1|+(b-$\frac{1}{2}$)2=0,则(a+2b)3的值是( )
| A. | 0 | B. | -8 | C. | 8 | D. | -1 |
1.下列各组式子中的两个单项式是同类项的是( )
| A. | 2x3与3x2 | B. | 12ax与8bx | C. | x4与a4 | D. | 23与-3 |
2.下列四组数据不能作为直角三角形的三边长的是( )
| A. | 6、8、10 | B. | 5、12、13 | C. | 7、10、12 | D. | 3、4、5 |
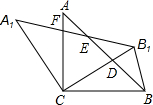 如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F
如图,在△ABC中,AC=BC,∠ACB=90°,将△ABC绕点C逆时针旋转α角(0°<α<90°),得到△A1B1C,连接BB1,设CB1交AB于D,A1B1分别交AB,AC于E,F